Предмет: Геометрия,
автор: Provokatsiya
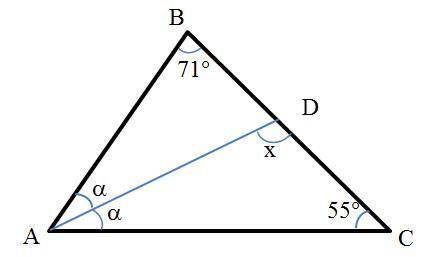
В треугольнике ABC проведена
биссектриса AD. Найди угол ADC,
если угол В равен 71°, а угол Сравен
55°.
B
D
А
C
Ответы
Автор ответа:
4
Ответ:
∠ADC = 98°
Объяснение:
Дано (см. рисунок):
ΔABC
∠B = 71°
∠C = 55°
AD - биссектриса
Найти: ∠ADC=x.
Решение.
Применим следующие известные свойства треугольников:
1) Сумма внутренних углов треугольника равна 180°.
2) Биссектриса угла треугольника делить пополам этот угол.
В ΔABC по свойству 1) имеем:
∠A+∠B+∠C = 180° или ∠A = 180°-∠B-∠C = 180° - 71° - 55° = 54°.
Биссектриса AD по свойству 2) делить пополам угол А, то
α = 54°:2 = 27°.
В ΔADC по свойству 1) имеем:
x+α+∠C = 180° или x = 180°-α-∠C = 180° - 27° - 55° = 98°.
Приложения:
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Биология,
автор: mikhailzyryano1
Предмет: Математика,
автор: koctakomry
Предмет: География,
автор: Кристина21062005
Предмет: Русский язык,
автор: koshmoro