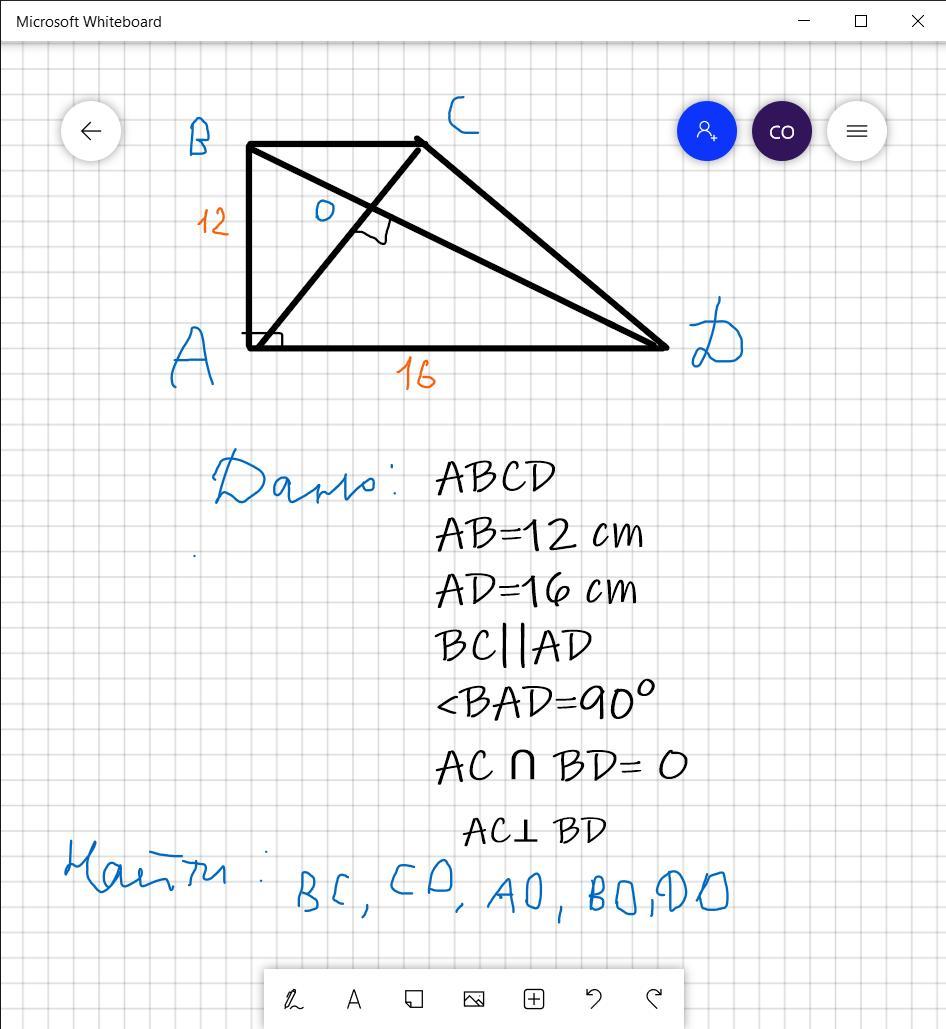
Диагонали прямоугольной трапеции ABCD взаимно перпендикулярны. Короткая боковая сторона AB равна 12 см, длинное основание AD равно 16 см.
Определи:
1. короткое основание BC:
BC=
см.
2. Длины отрезков, на которые делятся диагонали в точке пересечения O:
короткая диагональ делится на отрезки CO=
см и AO=
см;
длинная диагональ делится на отрезки BO=
см и DO=
сm
Ответы
Ответ: 9 см; 5,4 см; 9,6 см; 7,2 см; 12,8 см
Пошаговое объяснение:
на фото рисунок и дано
Прежде всего мы можем узнать ВД из ΔАВД
Это египетский треугольник, т.к. угол ВАД=90° и катеты соотносятся как 3:4 (12:16=3:4)
k=12/3=4
Поэтому гипотенуза ВД=5k=5*4=20 см
У трегольников ΔАВО и ΔАДО общая сторона--АО. Причем оба прямоугольные, поэтому по теореме Пифагора выводим катет АО из обоих треугольников.
из ΔАВО АО²=АВ²-ОВ²
из ΔАДО АО²=АД²-ОД²
АВ²-ОВ²=АД²-ОД²
И для удобства обозначим ОВ=х, ОД=20-х
12²-х²=16²-(20-х)²
144-х²=256-400+40х-х²
144=256-400+40х
40х=144+400-256
40х=288
х=7,2 см
ОВ=7,2 см
ОД=20-х=20-7,2=12,8 см
Теперь подставляем результат в формулу
АО²=АВ²-ОВ²
АО²=144-(7,2)²=92,16
АО=9,6 см
Т.к. ВС параллельна АД, то ВД--сечная, поэтому их внутренние разносторонние углы СВД и ВДА равны. Также известно, что ВОС=АОД (как вертикальные), из этого делаем вывод, что треугольники ΔДОА ~ΔВОС подобны
Поэтому ВС/АД=ВО/ОД
ВС=АД*ВО/ОД=16*7,2/12,8= 9 см
И, наконец, ОС/АО=ВС/АД
ОС=ОА*ВС/АД=5,4 см
Фотку с обозначеными сторонами тоже оставила