Предмет: Математика,
автор: rustammurr
срочно пожалуйста нужно
Приложения:
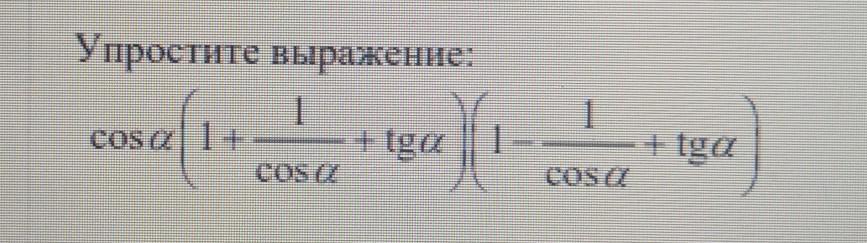
Ответы
Автор ответа:
1
Ответ:
упростим по формуле:
по формуле:
rustammurr:
а как тут можно ещё вопрос задать?
Похожие вопросы
Предмет: Алгебра,
автор: АнюТка161
Предмет: Алгебра,
автор: tchasick5778
Предмет: Химия,
автор: KatyaLaneeva
Предмет: Қазақ тiлi,
автор: kusayyn2006
Предмет: Математика,
автор: Энджи1111