Предмет: Математика,
автор: mikhailvinogradov201
Вычислите: фото прикреплено
Приложения:
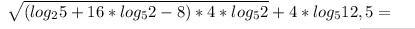
Ответы
Автор ответа:
0
Ответ:
ну не знаю
Пошаговое объяснение:
наверно 4657и 7
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: malishka15551
Предмет: Математика,
автор: arsenpogosyan
Предмет: Литература,
автор: remromyl
Предмет: Русский язык,
автор: Вероник65489
Предмет: Русский язык,
автор: sever2012bp3zjot