Помогите пожалуйста!
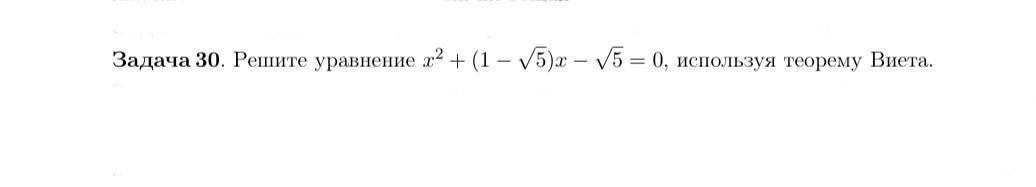
Ответы
Ответ: {-1;}
Объяснение:
вид любого квадратного уравнения: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
теорема виета: х1 + х2 = - b/a и x1*x2= c/a
( Сумма корней квадратного уравнения аx2 + bx + c = 0 равна отношению второго коэффициента к старшему, взятому с противоположным знáком, а произведение корней равно отношению свободного члена к старшему коэффициенту)
у нас приведенное уравнение, это значит, что старший коэффициент а=1.
соответственно для приведенного уравнения:
х1 + х2 = - b x1*x2= c
( Сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.)
в нашем уравнении средний коэффициент b = (1-), тогда х1+х2= -b = - (1-
) =
-1
а свободный член с = - , тогда х1*х2= -
.
Теперь осталось подобрать такие значения х1 и х2, сумма которых -1, а произведение равно -
. Подобрать достаточно легко, это числа
и -1 (можно подставить и посмотреть). Ну и все х1=
, а х2= -1