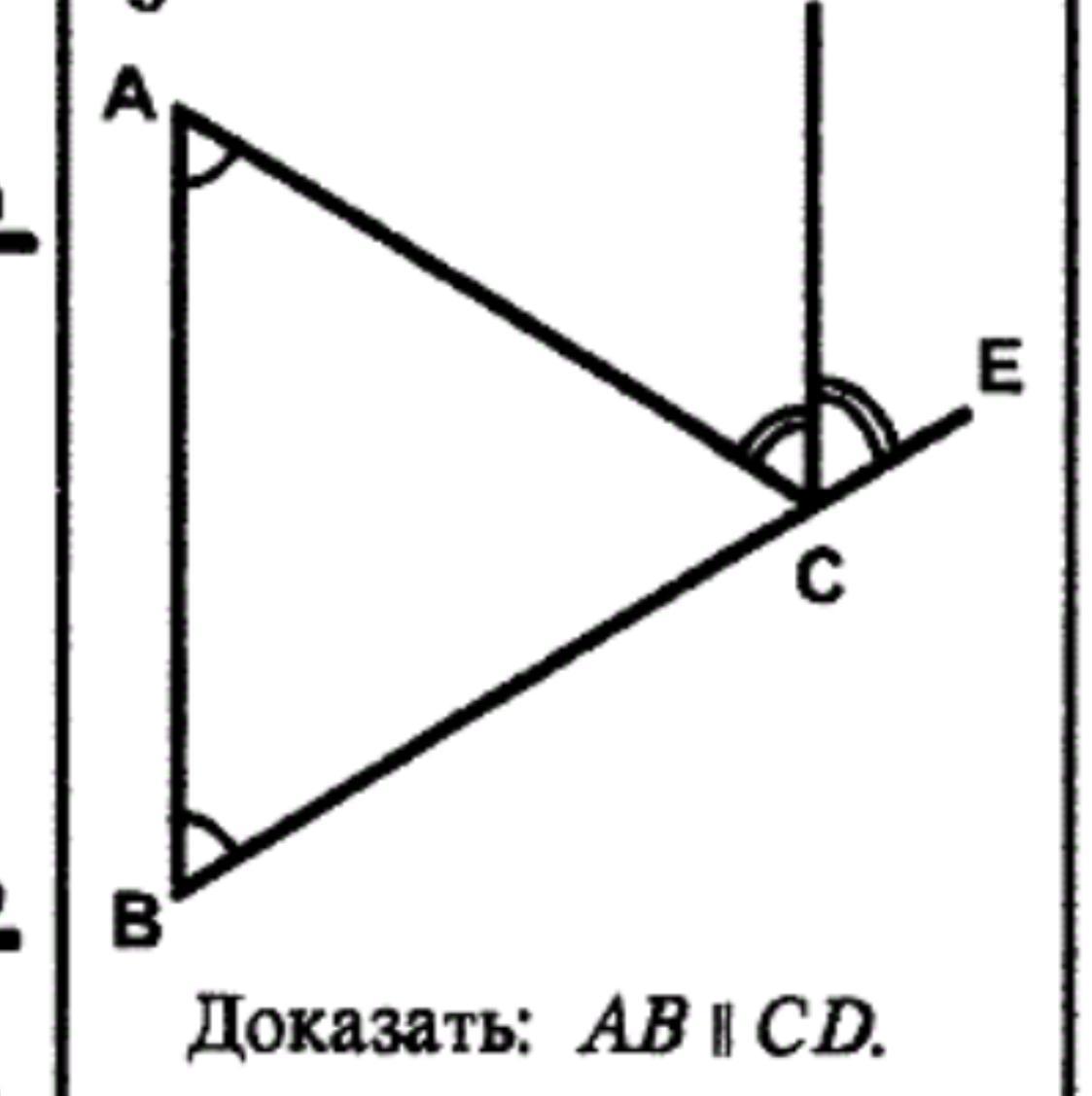
Решите пж задачу, не получается(((
Ответы
Ответ:
================================
Объяснение:
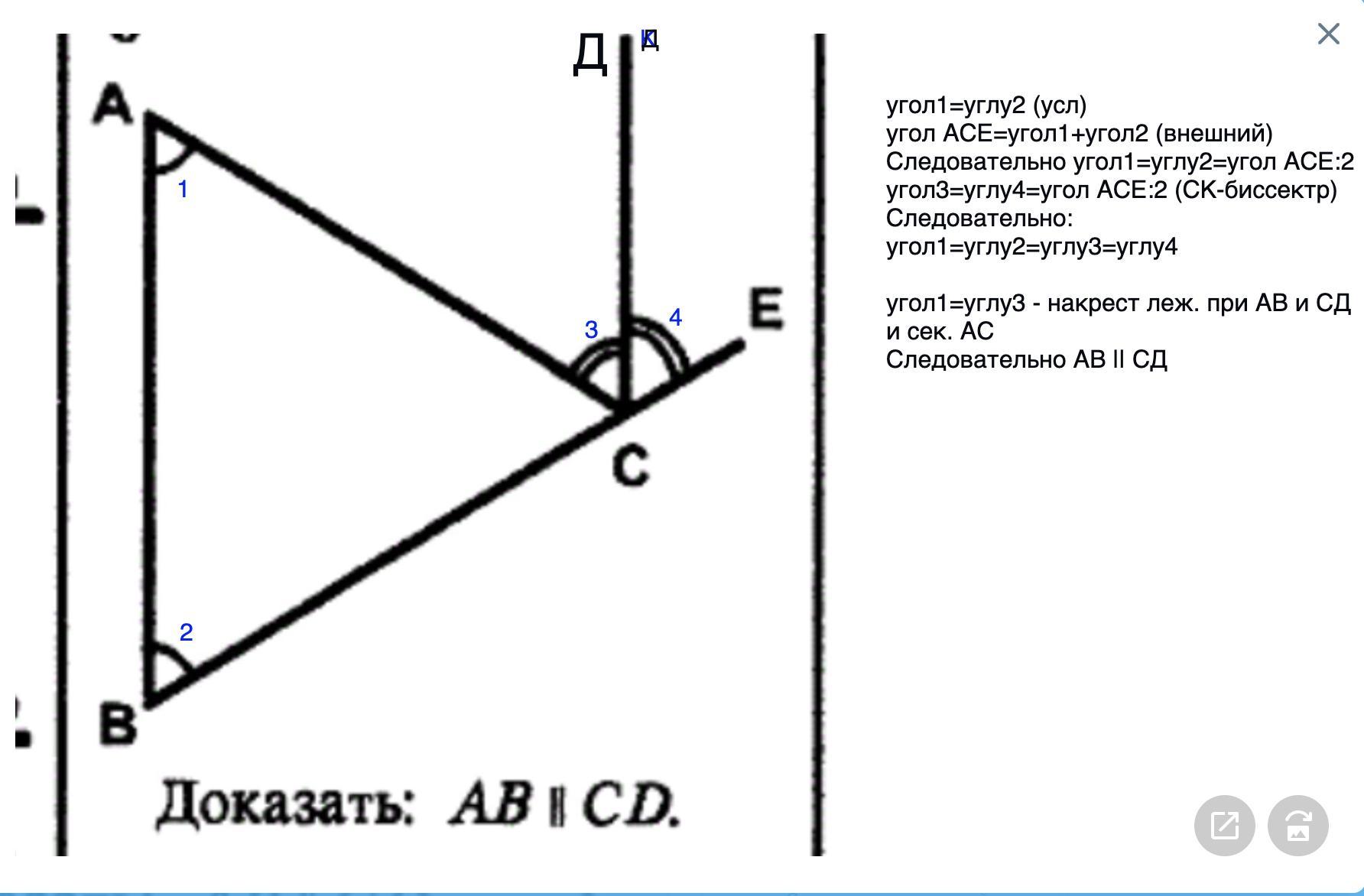
не особо понимаю откуда у нас ACE:2 взялось...
Ответ:
См. Объяснение
Объяснение:
Угол АСЕ по отношению к треугольнику АВС является внешним углом, который равен сумме углов А и В.
Действительно, так как сумма внутренних углов треугольника равна 180°, то:
∠АСВ = 180° - (∠А +∠В) = 180° - х - уравнение (1)
С другой стороны, так как угол ВСЕ - развёрнуты (равен 180 °), то:
∠АСВ = 180° - (∠АСD +∠DCE) = 180° - у - уравнение (2)
Так как в левой части уравнений (1) и (2) - одно и то же число, то из этого следует, что:
180° - х = 180° - у
х = у
(∠А +∠В) = (∠АСD +∠DCE).
Так как ∠А = ∠В и ∠АСD = ∠DCE,
то из этого следует, что ∠А = ∠В = ∠АСD = ∠DCE.
Так как ∠А и ∠АСD являются внутренними накрест лежащими углами при прямых АВ и СD и секущей АС, при этом ∠А = ∠АСD, то это означает, что АВ║CD (если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то такие прямые параллельны), - что и требовалось доказать.
Примечание.
Аналогично можно доказать параллельность прямых АВ и СD через равенство ∠В = ∠DCE, которые являются соответственными при прямых АВ и СD и секущей ВЕ: если при пересечении двух прямых третьей соответственные углы равны, то такие прямые параллельны. Следовательно, АВ║CD. Что и требовалось доказать.