Предмет: Геометрия,
автор: valentina09016111
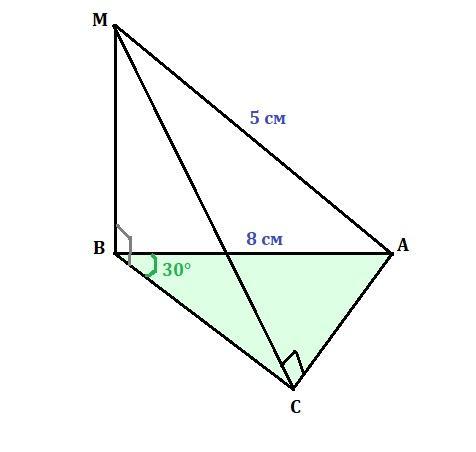
У прямокутному трикутнику ABC гіпотенуза AB = 8 см, ∠B = 30°. Через точку B проведено перпендикуляр BM до площини трикутника. Відстань від точки M до точки A дорівнює 5 см. Знайдіть відстань від точки M до точки C.
Ответы
Автор ответа:
2
Ответ:
3 cм
Объяснение:
Трикутник ABC. АВ - гіпотенуза ⇒ ∠АСВ=90°, ВС⊥АC.
- Якщо у прямокутному трикутнику один з гострих кутів дорівнює 30°, то протилежний цьому куту катет буде дорівнювати половині гіпотенузи
Катет см
МВ⊥(ABC), тому (за властивістю) вона перпендикулярна до кожної прямої, що належить площині ABC (трикутнику ABC), тобто MВ⊥BC.
Оскільки МВ – перпендикуляр до площини ABC, то MС – похила (точка С – основа похилої), а відрізок ВС – проекція похилої на площину ABC. Так як АС⊥ВC, то за теоремою «про три перпендикуляри» (якщо відрізок, який проведений через основу похилої перпендикулярний до похилої, то він перпендикулярний і до її проекції, і навпаки), тобто MС⊥АB.
ΔМСА - прямокутний. ∠МСА=90°. За теоремою Піфагора знайдемо довжину катета МС:
см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аделинка111111
Предмет: География,
автор: fed63802
Предмет: Русский язык,
автор: Карина144
Предмет: Математика,
автор: Dik0000