Question

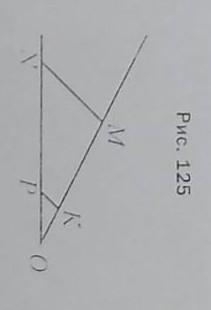
На рисунке 125 MN || KP, NP=20 см PO=8 см, MK=15 СМ. Найдите отрезок KO​

Answer 1

Ответ:

$\boxed{ KO = 6}$ см

Объяснение:

Дано: MN || KP, NP = 20 см, PO = 8 см, MK = 15 см

Найти: KO - ?

Решение: NO = NP + PO = 20 + 8 = 28 см. Пусть KO = x. MO = MK + KO =

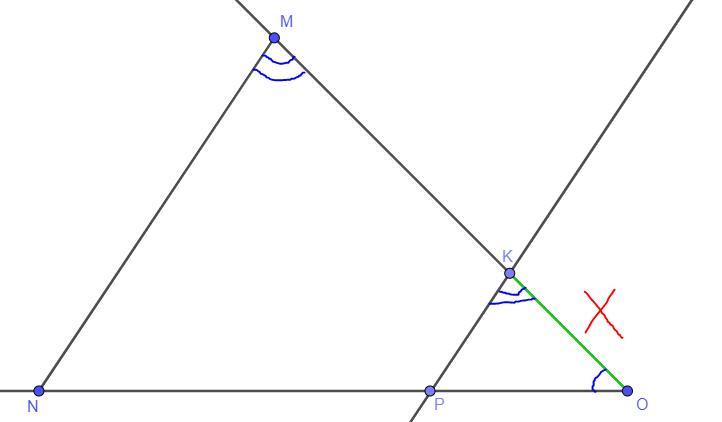
= 15 + x. Треугольник ΔKOP подобен треугольнику ΔMON по двум углам так угол ∠MON - общий, угол ∠OKP = ∠OMN как соответствующие углы при параллельных прямых(MN || KP - по условию) и секущей. Так как треугольник ΔKOP подобен треугольнику ΔMON, то $\frac{MO}{KO} = \frac{NO}{PO} \Longrightarrow MO * PO = KO * NO$.

MO * PO = KO * NO

8(15 + x) = 28x

120 + 8x = 28x

20x = 120|:20

x = 6

$KO = x = 6$ см.