Предмет: Математика,
автор: mgm16032004
Решите логарифмическое неравенство
Приложения:
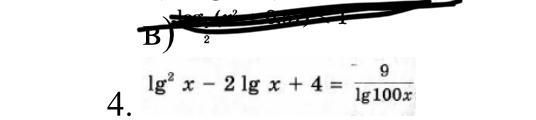
muhambek2004:
это ж уровнение
Ответы
Автор ответа:
1
Ответ:
ОДЗ: х>0
пусть lgx = t, lgx не равен -2.
Ответ: 10
Похожие вопросы
Предмет: Математика,
автор: ЧихляеваКатя
Предмет: Алгебра,
автор: krip300
Предмет: Математика,
автор: narminrustamli1
Предмет: Русский язык,
автор: PowerDrish2017
Предмет: Математика,
автор: Toma683