Предмет: Математика,
автор: ilnurgadilyaev
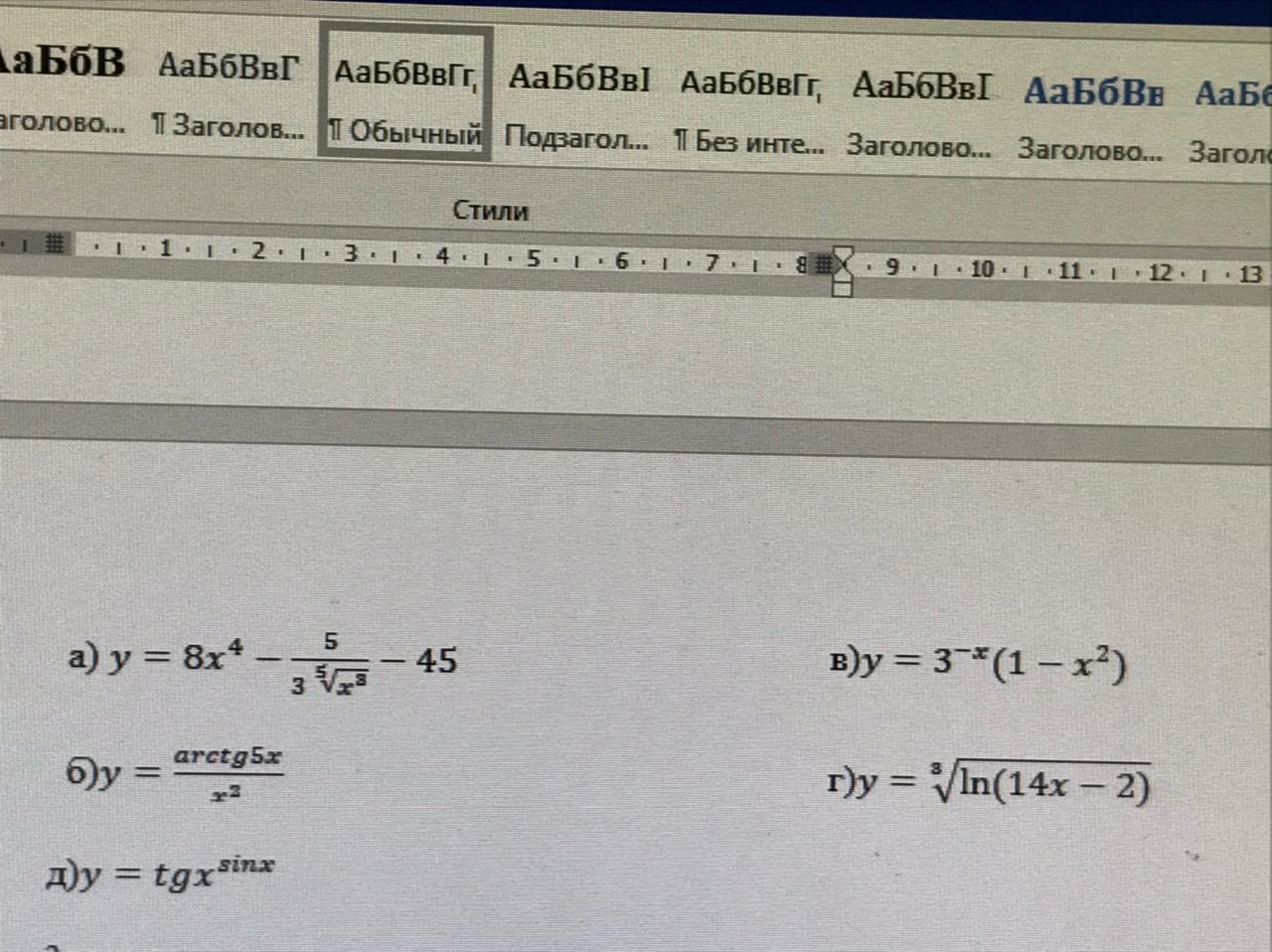
Найдите производные функции
Приложения:
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
a)
б)
в)
г)
д) здесь будем логарифмировать обе части
Похожие вопросы
Предмет: Химия,
автор: ewromash2014
Предмет: Математика,
автор: 1873979739407392830
Предмет: Русский язык,
автор: Dasha335
Предмет: Математика,
автор: Ksusha252006