Предмет: Математика,
автор: Stulinanastya
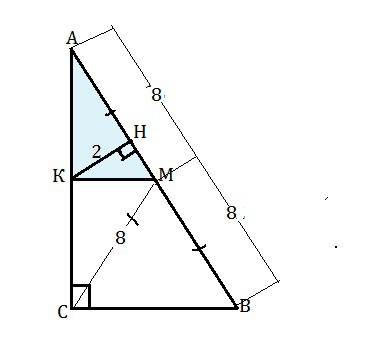
В прямоугольном треугольнике ABC медиана CM равна 8 см, а расстояние от середины катета AC до гипотенузы AB равно 2 см. Найдите площядь треугольника.
Ответы
Автор ответа:
0
Почему-то при решении задач с таким условием за расстояние от середины АС до гипотенузы принимают среднюю линию треугольника. Это неверно.
Расстояние от точки до прямой - длина проведенного из точки к прямой перпендикуляра.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине. ⇒ АМ=ВМ=8 см
АВ=8•2=16 см
Пусть середина АС - точка К. Тогда КМ соединяет середины двух сторон. КМ- средняя линия ∆ АВС.
Средняя линия треугольника параллельна третьей стороне и делит его на подобные треугольники.
КМ -параллельна ВС, угол АКМ=90º,
∆ АКМ - прямоугольный. КН его высота.
∆ АКМ~∆ АВС с коэффициентом подобия АМ:АВ= k=1/2
Площади подобных фигур относятся как квадрат коэффициента их подобия.
S∆ AKM:S∆ ABC=k²=1/4
S∆ ABC=4 S∆ AKM
Площадь ∆ АКМ=КН•AМ:2=2•8:2=8 см²
S∆ ABC=8•4=32 см²
Расстояние от точки до прямой - длина проведенного из точки к прямой перпендикуляра.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине. ⇒ АМ=ВМ=8 см
АВ=8•2=16 см
Пусть середина АС - точка К. Тогда КМ соединяет середины двух сторон. КМ- средняя линия ∆ АВС.
Средняя линия треугольника параллельна третьей стороне и делит его на подобные треугольники.
КМ -параллельна ВС, угол АКМ=90º,
∆ АКМ - прямоугольный. КН его высота.
∆ АКМ~∆ АВС с коэффициентом подобия АМ:АВ= k=1/2
Площади подобных фигур относятся как квадрат коэффициента их подобия.
S∆ AKM:S∆ ABC=k²=1/4
S∆ ABC=4 S∆ AKM
Площадь ∆ АКМ=КН•AМ:2=2•8:2=8 см²
S∆ ABC=8•4=32 см²
Приложения:
Похожие вопросы
Предмет: История,
автор: lenastarostina16
Предмет: Русский язык,
автор: ajdanaaueldek
Предмет: Алгебра,
автор: Ekaterinagalaeva2737
Предмет: Химия,
автор: Sasha86rus
Предмет: Обществознание,
автор: nika1998veronia