Предмет: Математика,
автор: dima2003121
тригонометрия 45 баллов
Приложения:
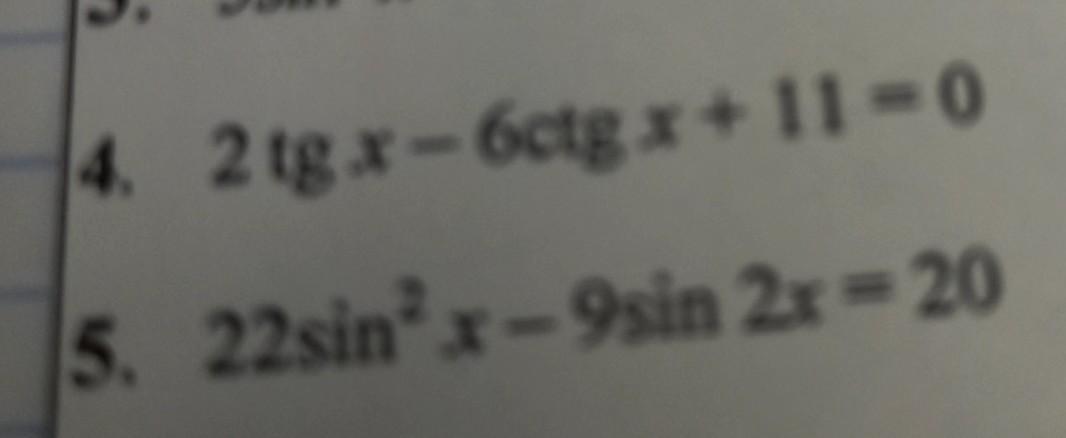
Ответы
Автор ответа:
2
Ответ:
4.
замена:
t не равно 0.
5.
разделим на cos^2x, не равный 0.
n принадлежит Z.
an6906529:
можешь и мне помочь ?
Похожие вопросы
Предмет: Биология,
автор: Sasara
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: Anna22220604
Предмет: Математика,
автор: oksi0908
Предмет: Математика,
автор: egor597