Предмет: Математика,
автор: anton8927486278
Помогите решить надо расписать фото прилогаеться
Приложения:
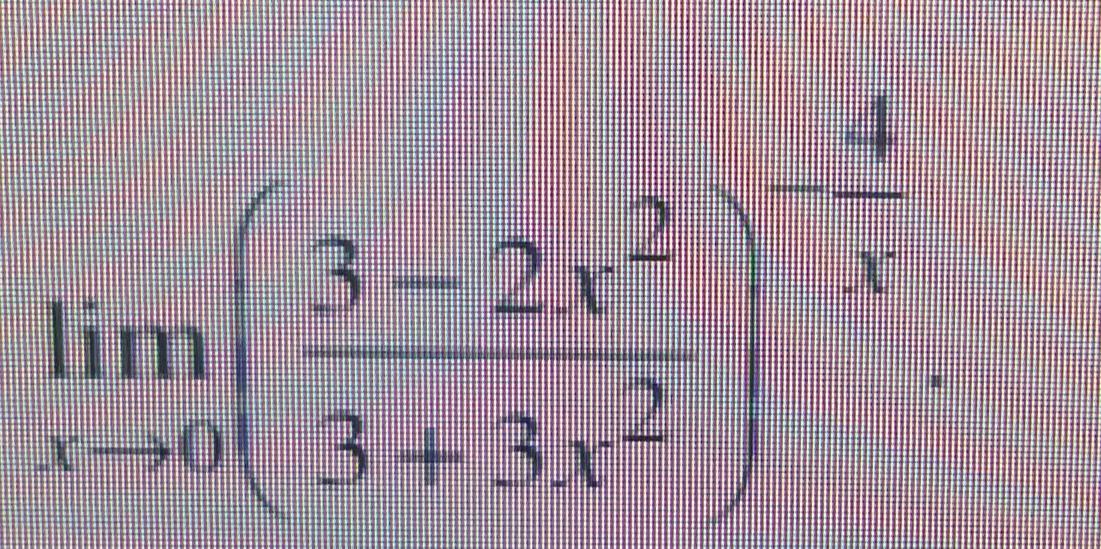
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Преобразуем выражение в скобках:
Подставим полученное выражение в исходное:
Функция натурального логарифма непрерывна, поэтому:
Найдём предел по правилу Лопиталя. Для этого найдём отдельно производные числителя и знаменателя дроби:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: drownemmett
Предмет: Русский язык,
автор: Orlova1996x
Предмет: Химия,
автор: dbaynazarova
Предмет: Русский язык,
автор: blvckcvt