Предмет: Алгебра,
автор: Аноним
помогите решить пределы. непрерывность
Приложения:
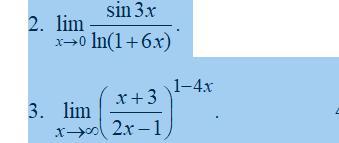
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: kurochkinaregi
Предмет: Физика,
автор: ka4елu
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Likaa04
Предмет: Математика,
автор: lera1154