Предмет: Математика,
автор: AndreyShaev
Здравствуйте помогите пожалуйста с математикой
№ 285(4), 286(2), 287(2)
Приложения:
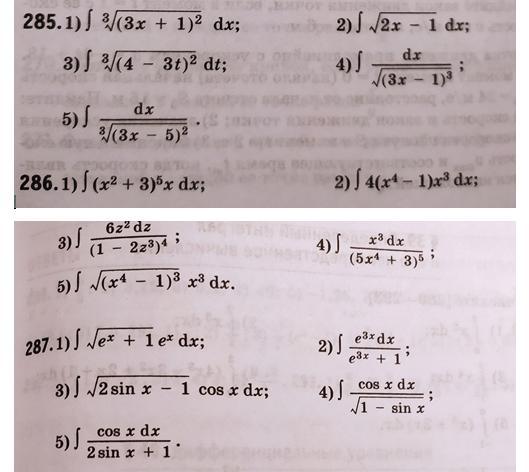
Ответы
Автор ответа:
1
Ответ:
285
4.
286
2.
287
2.
замена:
Похожие вопросы
Предмет: Русский язык,
автор: Thordimeena
Предмет: Русский язык,
автор: katyarau2006
Предмет: Литература,
автор: nadiaantonyshyn
Предмет: Математика,
автор: galimzhan0808p343i2
Предмет: Математика,
автор: dywcan