Предмет: Алгебра,
автор: kravcenkoaleksandr64
Найдите площадь земельного участка, предназначенного под строительство загородного дома, если его ширина на 7 метров меньше длины. Кроме того, известно, что размер этого участка по диагонали равен 13 метрам.
Ответы
Автор ответа:
0
Судя по условию, участок - прямоугольной формы (если было бы иначе, то решить было бы очень трудно).
Пусть участок - прямоугольник АВСD (см. рис.), его ширина ВС = х м, тогда длина АВ = (х + 7) м. Т.к. диагональ АС = 13 м, то, пользуясь теоремой Пифагора, составим и решим уравнение:
х² + (х + 7)² = 13²,
х² + х² + 14х + 49 = 169,
2х² + 14х + 49 - 169 = 0,
2х² + 14х - 120 =0,
х² + 7х - 60 = 0,
D = 7² - 4 · 1 · (-60) = 49 + 240 = 289; √289 = 17,
х₁ = (-7 + 17)/(2 · 1) = 10/2 = 5,
х₂ = (-7 - 17)/(2 · 1) = -24/2 < 0 - не подходит по условию задачи.
Значит, ширина прямоугольника равнв 5 м, а длина 5 + 7 = 12 (м).
Т.к. площадь прямоугольника равна произведению длины и ширины, то площадь данного участка равна 5 · 12 = 60 (м²).
Ответ : 60 м².
Приложения:
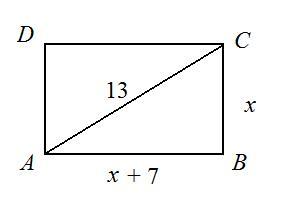
Похожие вопросы
Предмет: Физика,
автор: marjonakasimova
Предмет: Математика,
автор: animate137
Предмет: География,
автор: рита37037
Предмет: Математика,
автор: Аноним