Предмет: Алгебра,
автор: voleinik79
Нахождение значения функции по
значению аргумента и наоборот.
Урок 1
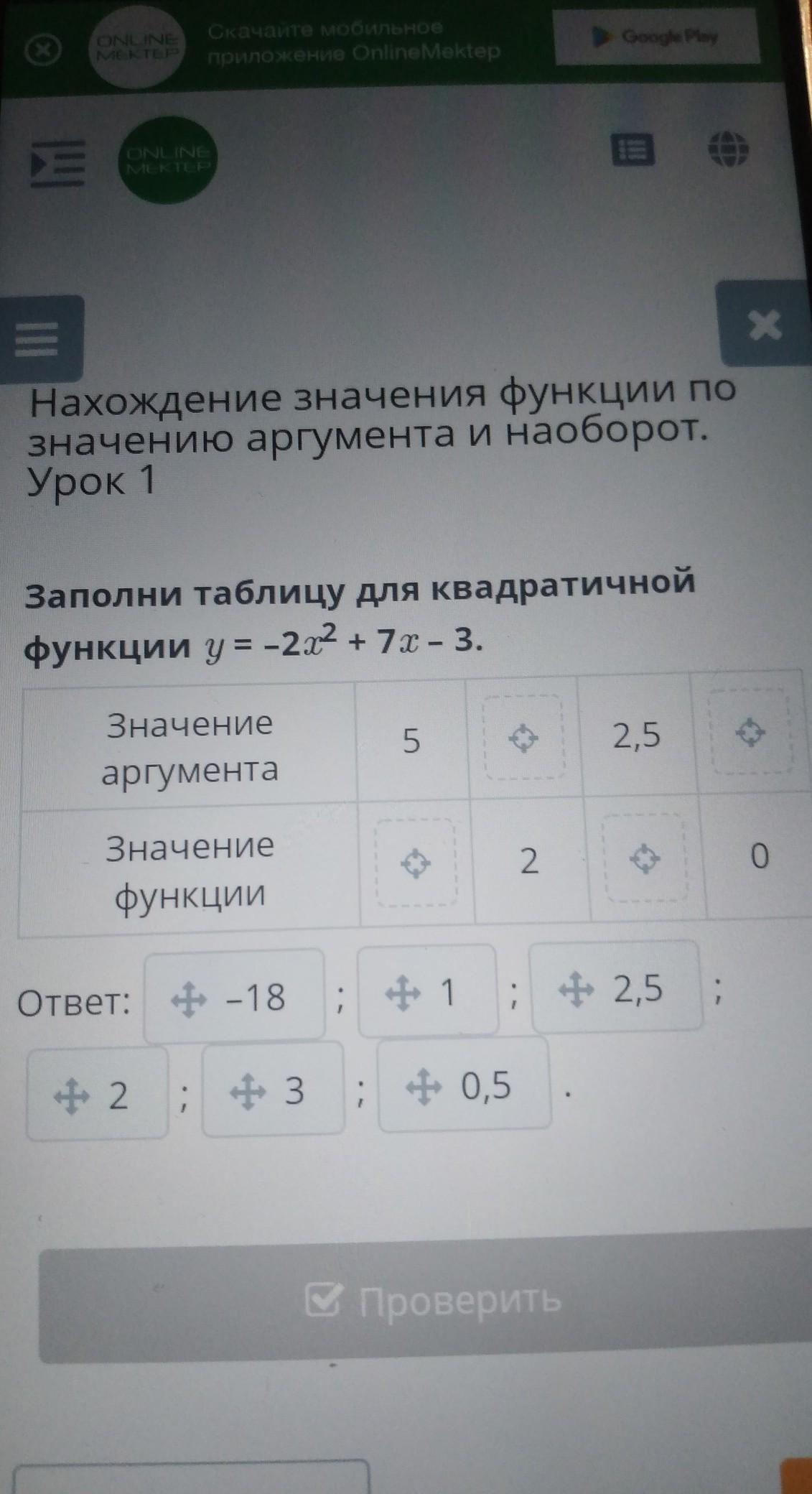
Заполни таблицу для квадратичной
функции y = -22 + 77-3.
Значение
аргумента
5
2,5
Значение
функции
2
0
Ответ: -18
1
: 2,5
;
- 2
: + 3 ; + 0,5
это 6 вопрос если можно то 7,8,9 ответы
незнаете ответ не отвечайте
Приложения:
Ответы
Автор ответа:
0
Объяснение:
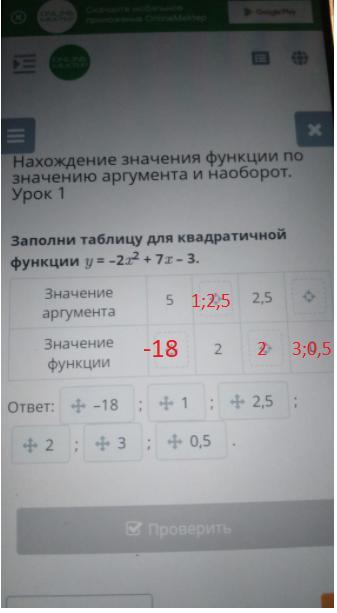
По условию значение аргумента равно 5, то х=5. Подставим данное значение и найдем значение функции
Значение функции y=2. Тогда подставим данное значение и решим уравнение
Чтобы записать смешанное число в виде неправильной дроби можно:
1)знаменатель умножить на целую часть;
2) к произведению прибавить числитель дробной части;
3) полученную сумму записать в числитель, а знаменатель оставить без изменений.
Далее по условию
Найдем значение функции
Значение функции равно 0, тогда
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: NiGGaTiV
Предмет: Математика,
автор: smosmo2015
Предмет: Химия,
автор: Chalova1
Предмет: Математика,
автор: Sandra2007Sandra