Предмет: Алгебра,
автор: znanija22228
СРОЧНО! 40 баллов .логарифм. неравенствa- решить пошагово с ОДЗ (и желательно с интервалом).
Приложения:
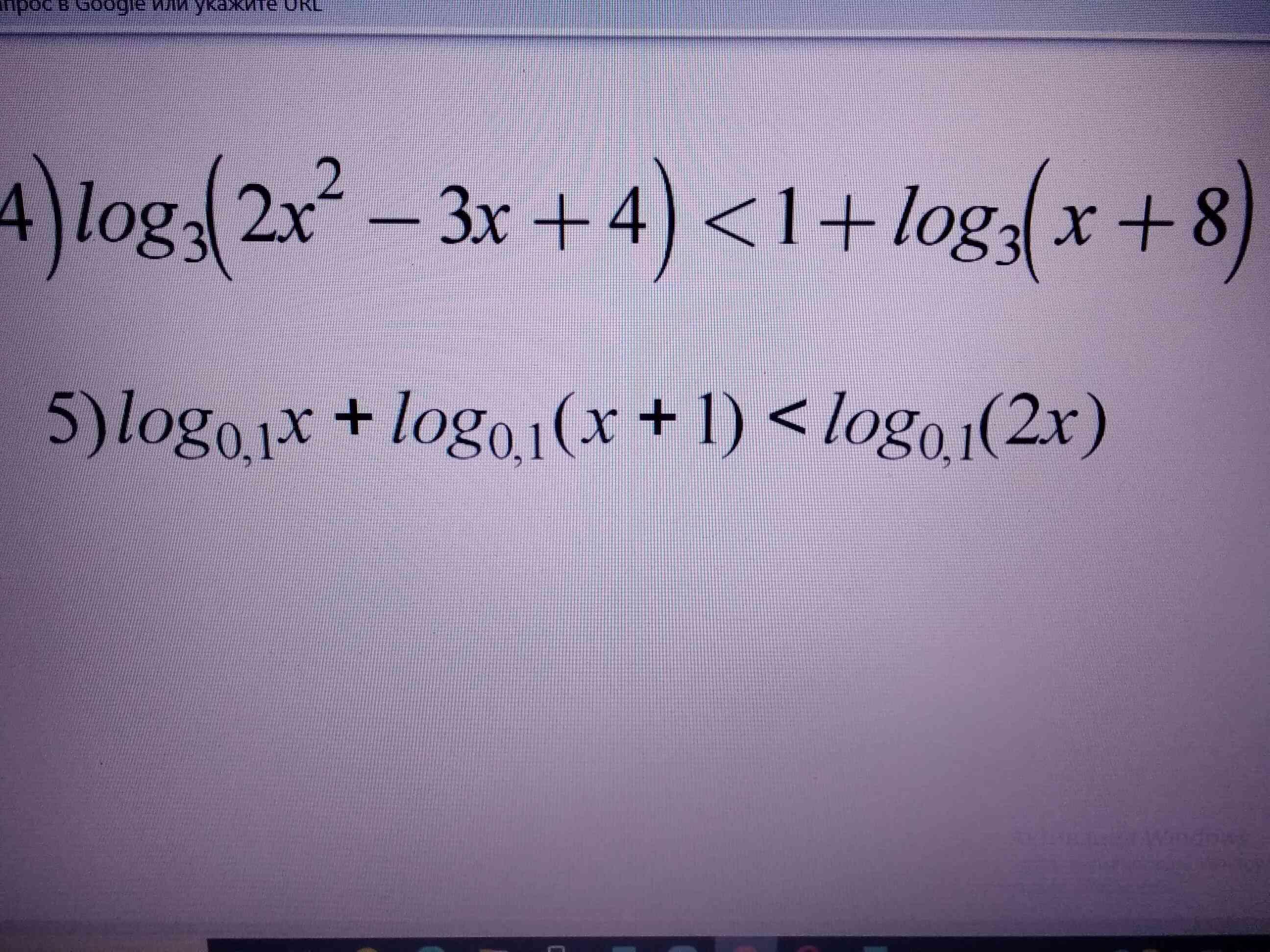
Ответы
Автор ответа:
2
__ODZ_ -8__+___-2__-___5_+__
Ответ с учетом ODZ: x∈ (-2;5)
C учетом ODZ: x∈ (1;+∞)
Автор ответа:
1
Ответ:
=============================
Объяснение:
Приложения:
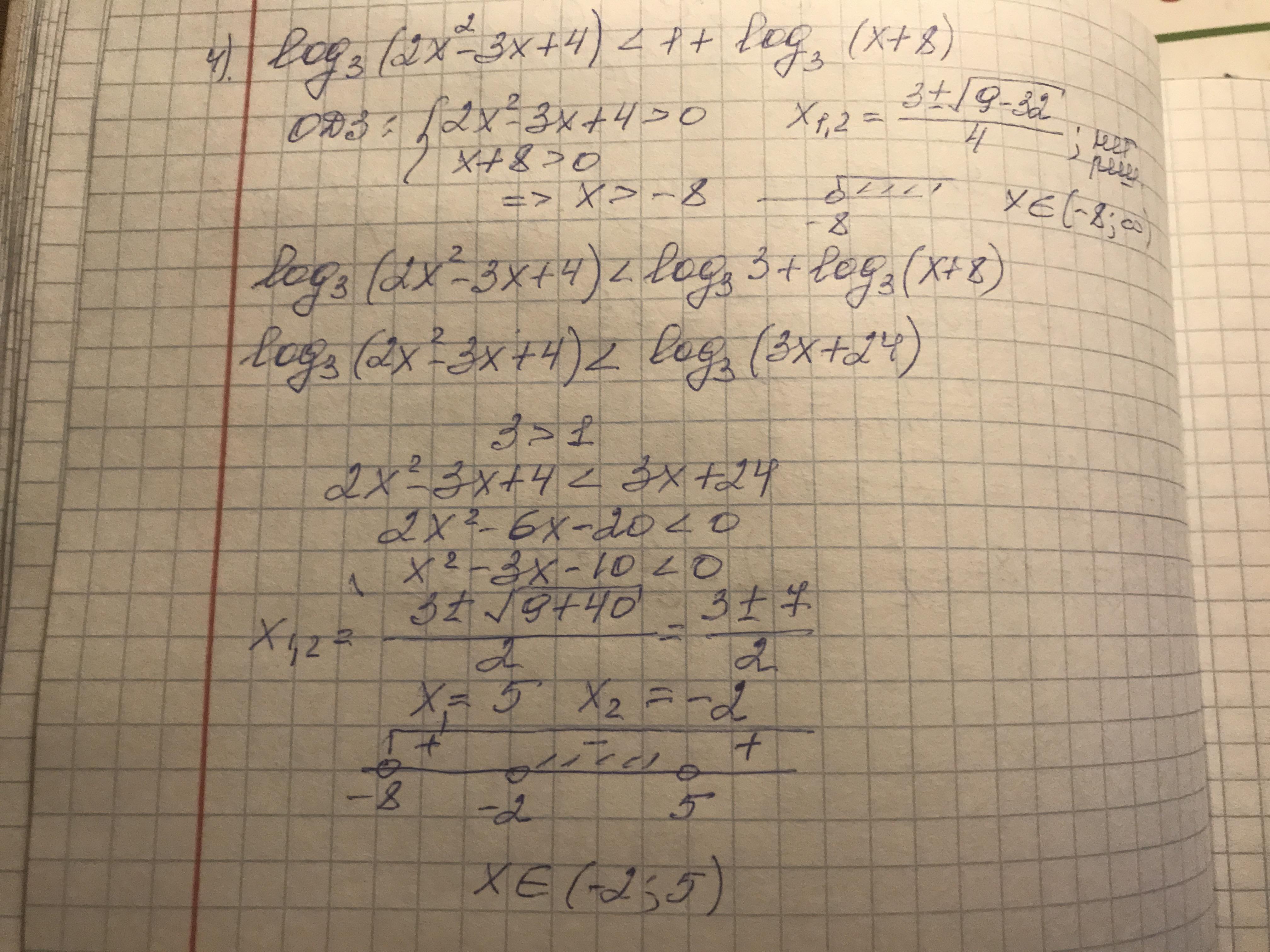
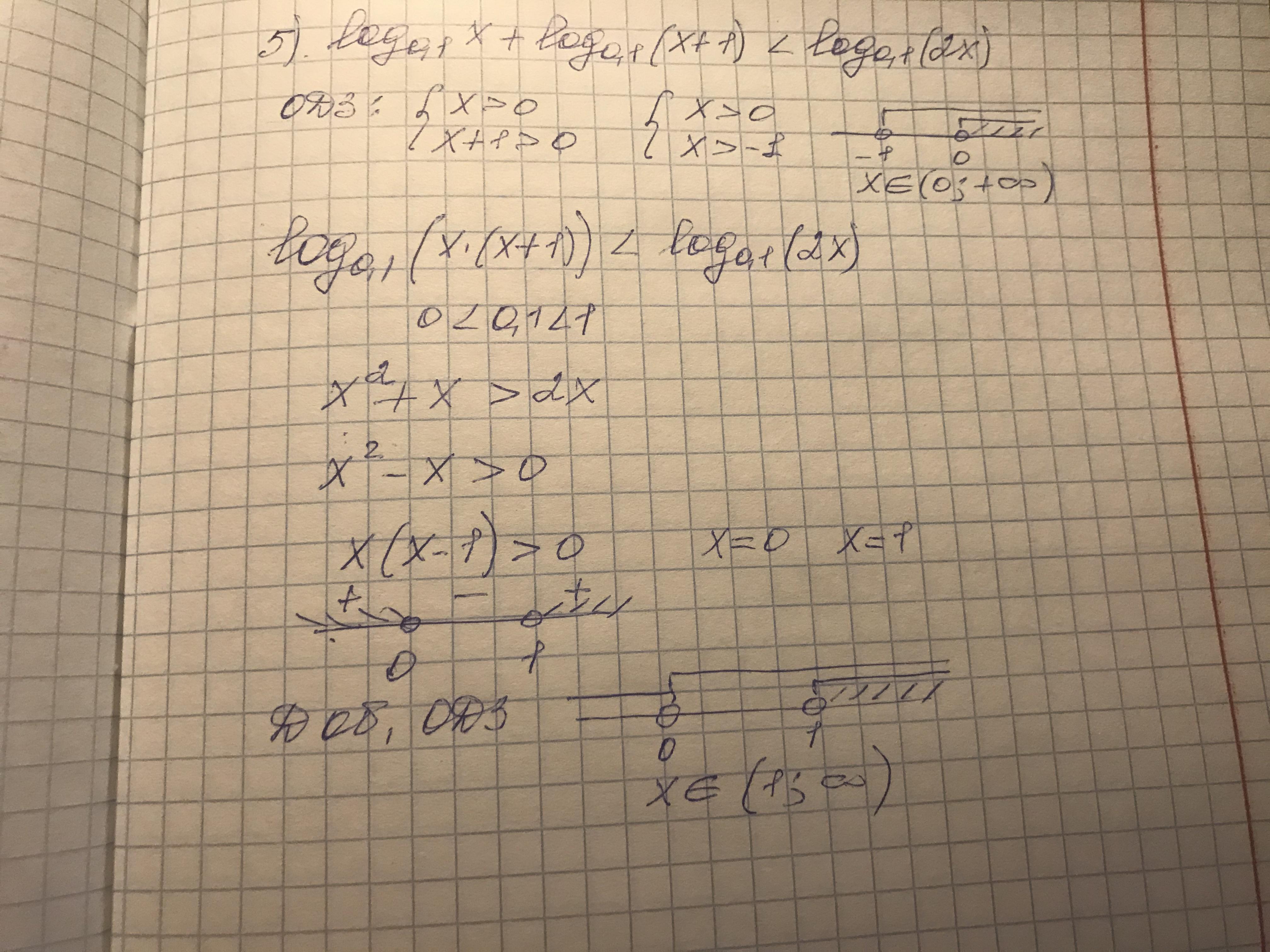
znanija22228:
Наталья, спасибо вам большое за помощь!)
Похожие вопросы
Предмет: Математика,
автор: mukhtasipova962
Предмет: Химия,
автор: mkornya
Предмет: Математика,
автор: servisemailru
Предмет: Русский язык,
автор: savchicz72