Предмет: Алгебра,
автор: znanija22228
СРОЧНО! 40 баллов .логарифм. неравенствa- решить пошагово с ОДЗ (и желательно с интервалом)
Приложения:
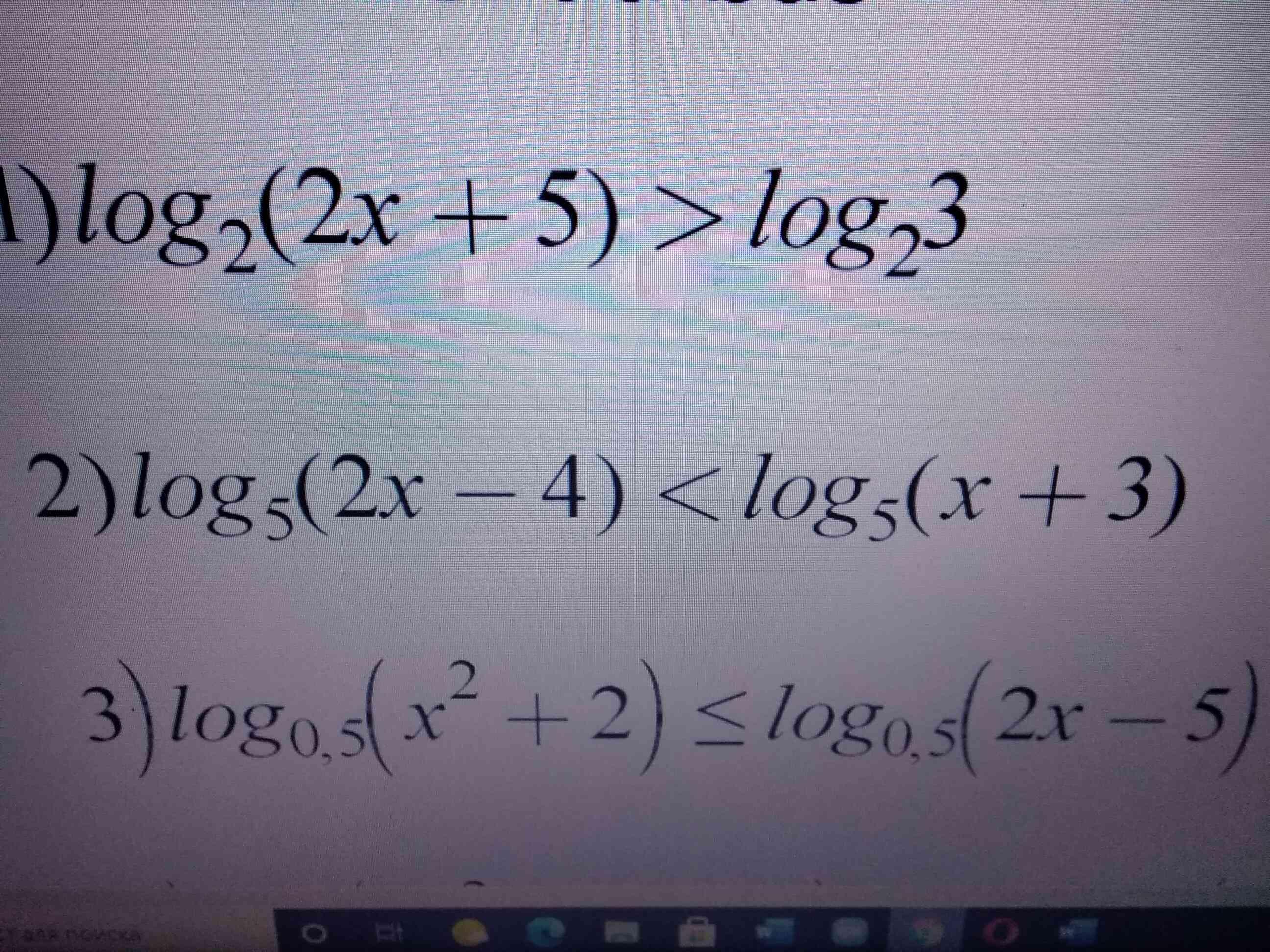
znanija22228:
3) неравенство не нужно решать
Ответы
Автор ответа:
1
1)
с учетом ОDZ x∈(-1;+oo)
2)
с учетом ODZ : x∈(2;7)
3)
Значит
С учетом ODZ: x∈(5/2;+∞)
огромное спасибо :)
Похожие вопросы
Предмет: Русский язык,
автор: gribkova98
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: mirskovvlad
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: 1234567890йцуз