Предмет: Алгебра,
автор: cerber
Найти S фигуры, ограниченной линиями:
у=х^2-4x, y=x-4 (При помощи интеграла)
Ответы
Автор ответа:
0
x^2-4x=x-4
x^2-5x+4=0
x1=1
x2=4
Приложения:
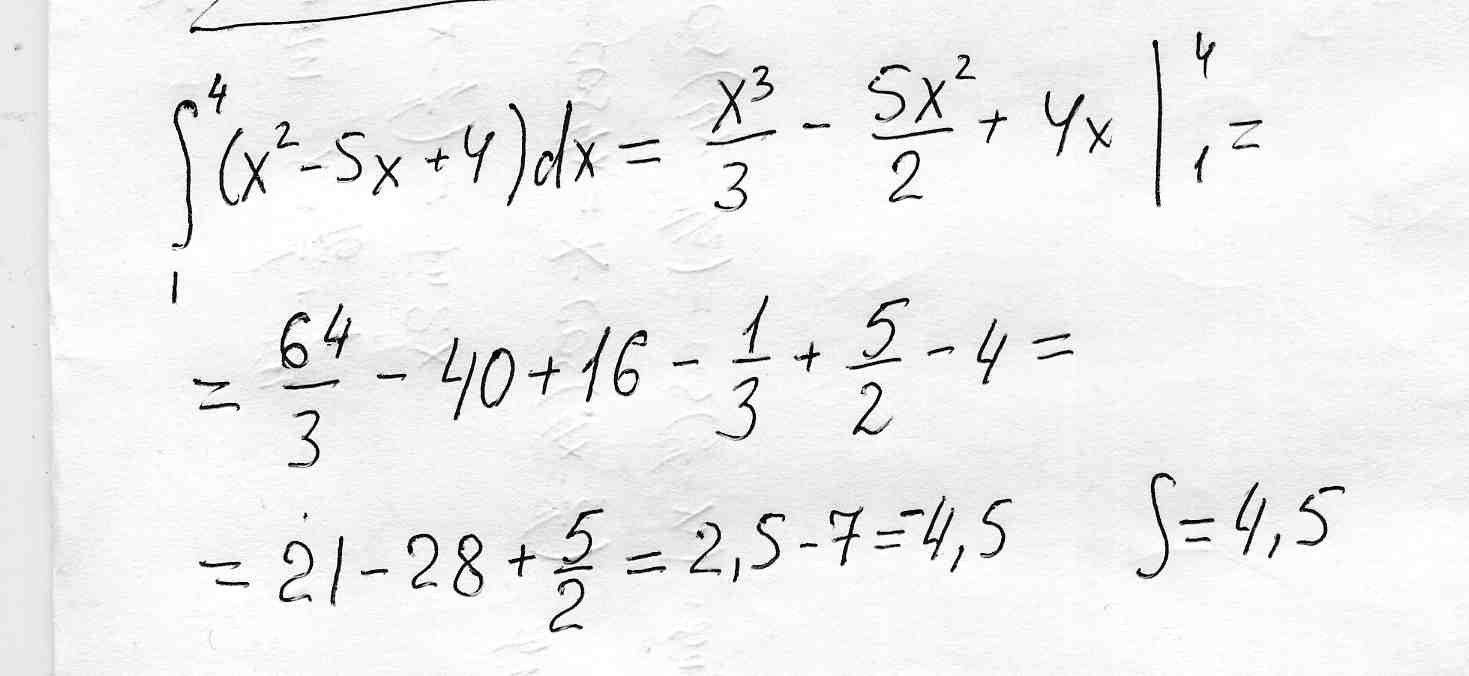
Автор ответа:
0
х²-4x=x-4
x²-5x+4=0
x²-x-4x+4=0
x(x-1)-4(x-1)=0
(x-4)(x-1)=0
x=4 ∨ x=1
Приложения:
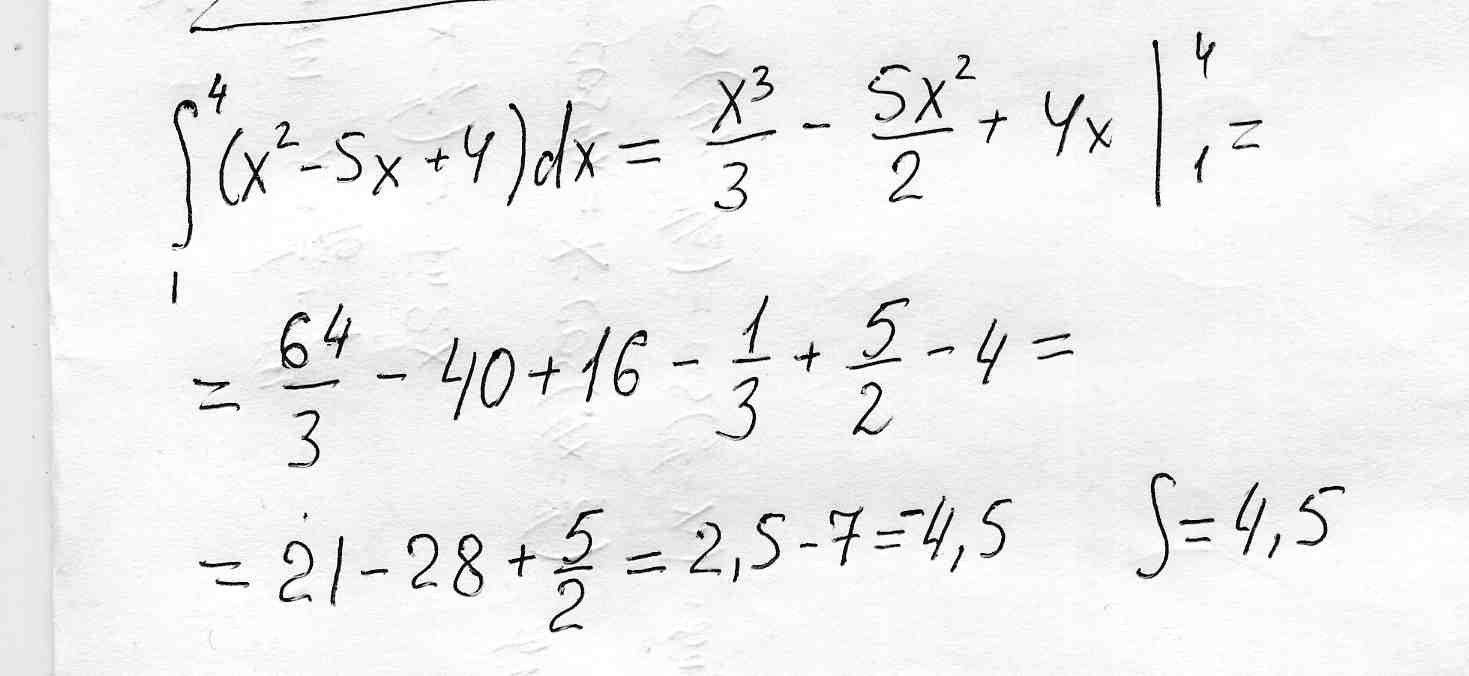
Похожие вопросы
Предмет: Математика,
автор: riga2pi
Предмет: Математика,
автор: elenagrzyb19
Предмет: Химия,
автор: aschuck085
Предмет: Алгебра,
автор: 89601632220
Предмет: Алгебра,
автор: Милая1995