Предмет: Математика,
автор: JesusChrismas
Частные производные и ещё какая-то дичь. Решите все, пожалуйста.
Приложения:
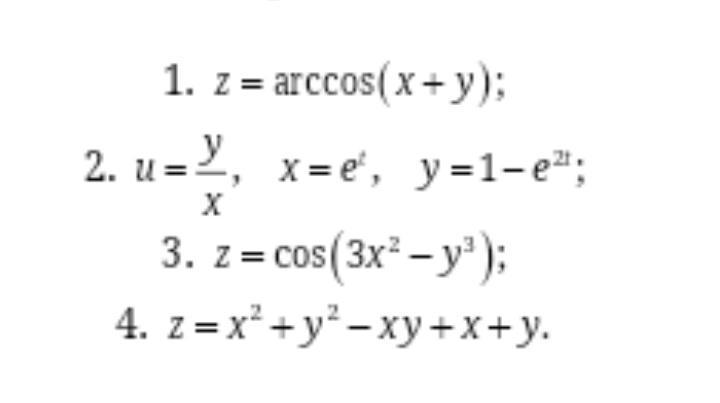
Ответы
Автор ответа:
1
Ответ:
1.
2.
формула:
3.
4.
JesusChrismas:
Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: Maksim13455
Предмет: Математика,
автор: fudd02
Предмет: Русский язык,
автор: прора
Предмет: Химия,
автор: Ира2807
Предмет: Алгебра,
автор: Nikita555000