Question

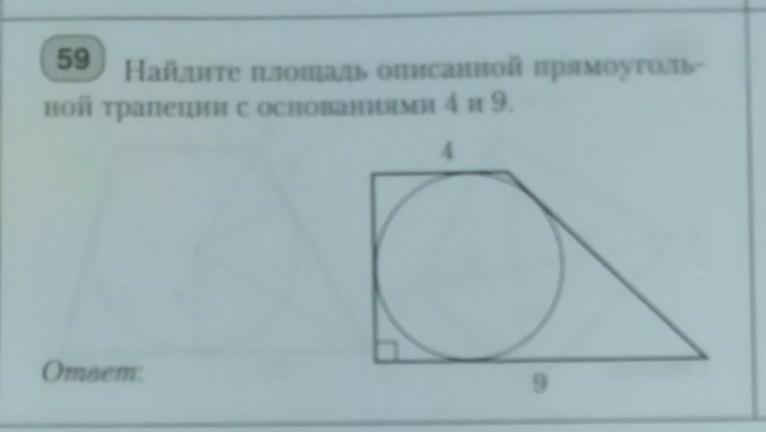
Помогите пожалуйста решить эту задачу по геометрии
​

Answer 1

Ответ:

Вспомним, что четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны между собой.  

Значит, сумма боковых сторон равна 4+9=13

Пусть дана трапеция АВСД,

ВС||АД, углы А и В - прямые.  

Опустим из С высоту СН на основание АД.  

Тогда АВСН - прямоугольник, АН=ВС=3, АВ=СН=х, СД=13-х. По т.Пифагора найдем х:

(13-х)²=х²+5²

169-26х=х²=х²+25  

26х=144  

х=144/26 Площадь трапеции равна половине произведения высоты на полусумму оснований:

S=CH*(ВС+АД):2 S=(144/26)*13/2=36 (ед. площади)

Объяснение: