Предмет: Алгебра,
автор: Pokutarik
Логарифмы. Помогите.
Приложения:
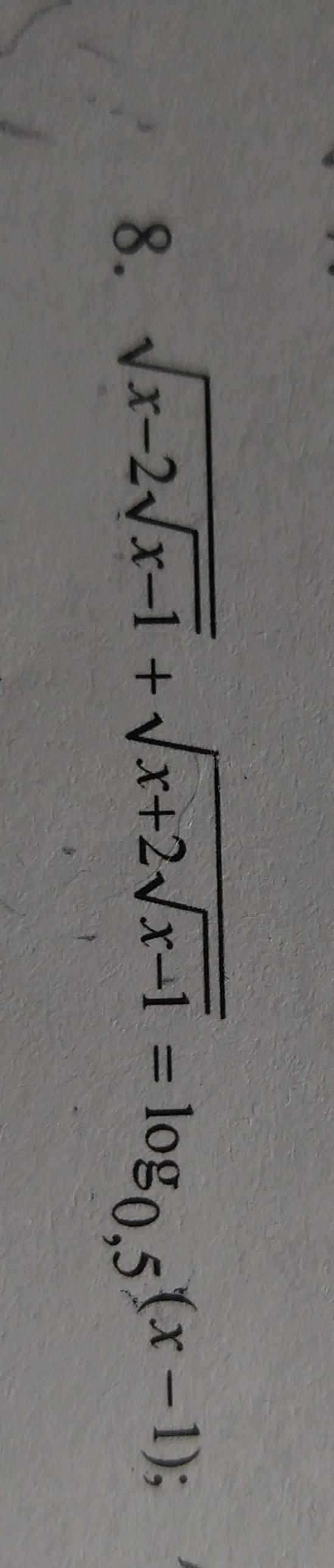
Ответы
Автор ответа:
1
ОДЗ: x-1>0; x>1
раскроем модули
при ОДЗ x>1 второе подмодульное выражение всегда положительно
рассмотрим первый модуль
рассмотрим условие где x∈(1;2)
по условию корень подходит
рассмотрим условие где x≥2
выполним замену √x-1 =t
тогда получаем
введем две функции f(t)=t прямая, возрастающая
и g(t)=log₀.₅t логарифмическая фукнция убывающая.
если построить их то мы увидим один корерь на промежутке от 0 до 1
тогда 0<√x-1<1; 0<x-1<1; 1<x<2
но по нашему условию х≥2
таким образом корень есть но нам не подходит
Ответ х=1,25
katerinabogomaz2000:
Не могла бы ты посмотреть задание у меня в ленте, пожалуйста
Похожие вопросы
Предмет: Математика,
автор: 2диман2
Предмет: Русский язык,
автор: учиница3
Предмет: Русский язык,
автор: Marliiin
Предмет: Алгебра,
автор: Nikespr
Предмет: Математика,
автор: Аноним