Предмет: Геометрия,
автор: falileevaulia4
1. Найдите две стороны треугольника, если их разность равна 28 см, а биссектриса,
проведенная к третьей стороне, делит ее на отрезки 43 см и 29 см.
2. В остроугольном треугольнике АВС его высоты ВД и АЕ пересекаются в точке О.
Докажите, что ВО ОД= АО OE.
Пожалуйста решите
Ответы
Автор ответа:
1
Ответ:
1)Обозначим треугольник АВС. (см. рисунок)
ВК- биссектриса,
Примем ВС=а, тогда АВ=а+28,
АК=43, КС=29
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам. (свойство биссектрисы).
АК:КС=АВ:ВС. ⇒
43:29=(а+28):а ⇒
43а=29а+28•29
14а=28•29 ⇒
а=2•29=58 см – длина ВС
58+28=86 см – длина АВ
2)
Приложения:
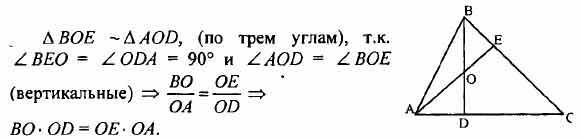
abdukarimov007:
пожалуйста, дай лучший ответ
Похожие вопросы
Предмет: Физика,
автор: irilagutina
Предмет: Русский язык,
автор: innesaeduardov
Предмет: Математика,
автор: avstria
Предмет: Физика,
автор: EvilGam3rProYT