Question

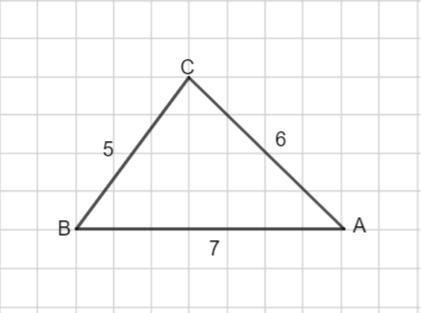
Найдите площадь треугольника, стороны которого равны 5., 6., 7.,


​

Answer 1

Ответ:

6√6 кв. ед.

Объяснение:

Найдем площадь треугольника по формуле Герона.

$S=\sqrt{p(p-a)(p-b)(p-c)} \\\\p=\dfrac{a+b+c}{2}$

где $a,b,c-$ стороны треугольника.

По условию a=5 ед.,b= 6 ед., c=7 ед.

Тогда найдем полупериметр.

$p=\dfrac{5+6+7}{2} =\dfrac{18}{2} =9$

Тогда площадь будет

$S=\sqrt{9(9-5)(9-6)(9-7)} =\sqrt{9\cdot 4\cdot 3\cdot 2} =3\cdot 2\sqrt{6} =6\sqrt{6}$

Значит, площадь треугольника равна 6√6 кв. ед.