Предмет: Алгебра,
автор: mashalove511
Помогите, пожалуйста, решить систему
Приложения:
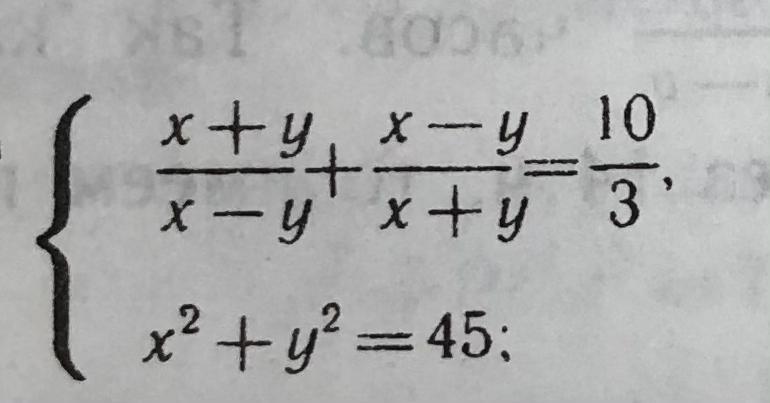
Ответы
Автор ответа:
2
преобразуем второе равенство
теперь преобразуем первое равенство
выполним подстановку
теперь получили новую систему
теперь найдем у
аналогично при х= -6
Ответы (6;-3) (6;3) (-6;-3)(-6;3)
mashalove511:
Большое спасибо
здравствуйте можете помочь мне с алгеброй зайдите на мой вопрос пожалуйста
Похожие вопросы
Предмет: История,
автор: darysha8
Предмет: Математика,
автор: 89145678100321314204
Предмет: Английский язык,
автор: kostyakosintse
Предмет: Қазақ тiлi,
автор: zhusupov06