Предмет: Геометрия,
автор: qwerty1poiu
Найди координаты точки пересечения для графиков двух функций. Первой записывай абсциссу этой точки.
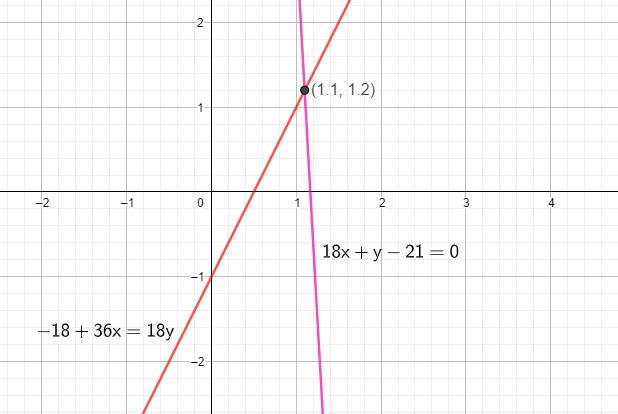
−18+36x=18y и 18x+y−21=0.
(В ответе запиши десятичную дробь, не ставь точку после неё.)
Ответ: x= y=
Ответы
Автор ответа:
1
Ответ:
(1,1;1,2)
Объяснение:
Для нахождения координаты точки пересечения для графиков двух функций, которые являются прямыми, составим систему уравнений:
Координаты точки (1,1;1,2) ⇔
Приложения:
Похожие вопросы
Предмет: Математика,
автор: vitaeva78
Предмет: Математика,
автор: annagul327
Предмет: Русский язык,
автор: 666AngelDemon666
Предмет: Физика,
автор: svyatoslavik
Предмет: Английский язык,
автор: Katyaflor