Предмет: Геометрия,
автор: ytytyu
Помогите пожалуйста! Дам 40 баллов
Надеюсь тут есть математики :)
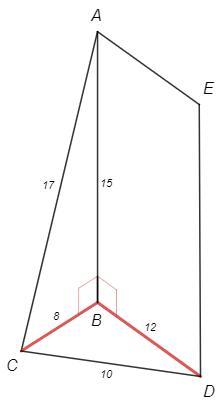
Найдите угол между плоскостями треугольника АВС и прямоугольника АВDЕ, если АВ=15 см, ВD=12 см, АС=17 см, ВС=8 см, СD=10 см.
С полным обьяснением пожалуйста :3
siestarjoki:
17^2 =8^2 +15^2 => ABC=90
Угол между плоскостями - угол между перпендикулярами к общей прямой AB. То есть угол CBD, по теореме косинусов.
cos(CBD) =9/16
Спасибо!
Ответы
Автор ответа:
1
Для сторон треугольника ABC выполняется теорема Пифагора
17^2 =8^2 +15^2
Следовательно, ∠ABC=90
∠ABD=90 (угол прямоугольника)
Угол между плоскостями - угол между перпендикулярами к общей прямой (AB).
Угол ∠CBD - искомый.
△CBD, теорема косинусов
cos(CBD) =(BC^2 +BD^2 -CD^2)/2BC*BD =(64+144-100)/2*8*12 =9/16
∠CBD =arccos(9/16)
Приложения:
Огромное спасибо!!!
Похожие вопросы
Предмет: Русский язык,
автор: innapro2005
Предмет: Химия,
автор: DanaBondarenkoS
Предмет: Геометрия,
автор: ZayacZnaniy
Предмет: ОБЖ,
автор: postmka
Предмет: Русский язык,
автор: Violetta546