Предмет: Математика,
автор: glebokkamyshkin
С помощью логарифмического дифференцирования вычислите производные данных функций:
Приложения:
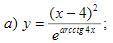
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
теперь посчитаем производную от этой дроби
подставляем производные из квадратных скобок в последнюю дробь и получаем
теперь подставим это в саму начальную формулу и не забудем про множитель 2
Похожие вопросы
Предмет: Обществознание,
автор: irina2004200420
Предмет: Математика,
автор: ЛеночкаБ
Предмет: Алгебра,
автор: skubster
Предмет: Другие предметы,
автор: Юлия25700
Предмет: География,
автор: Вика26062016