4) (a +1)(a-1)(a²-a+1)(a²+a+1)(a⁶+1)(a¹²+1)(a²⁴+1)
4, пожалуйста, "спростіть вираз" ("упростить")
25 баллов
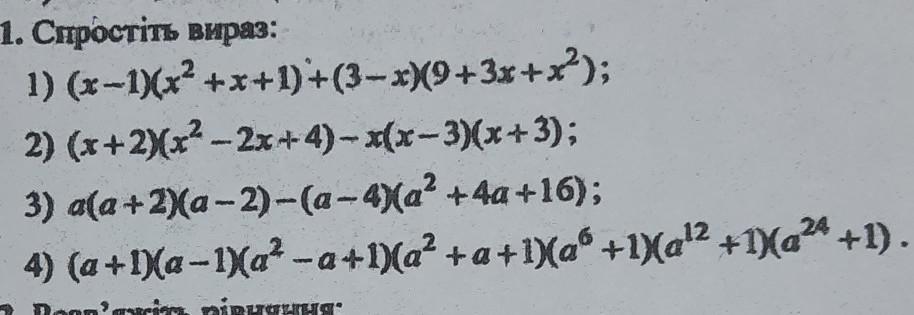
Ответы
Ответ:
Используем формулы сокращенного умножения
a² - b² = (a - b)(a + b)
a³ - b³ = (a - b)(a² + ab + b²)
a³ + b³ = (a + b)(a² - ab + b²)
1/
(x - 2)(x² + 2x + 4) - (1 + x)(x² - x + 1) = (x³ - 2³) - (x³ + 1) = -9
2/
(x - 3)(x² + 3x + 9) - x(x + 1)(x - 1) = (x³ - 3³) - x(x² - 1²) = x³ - 27 - x³ + x = x - 27
3/
a(a - 3)(a + 3) - (a + 2)(a² - 2a + 4) = a(a² - 3²) - (a³ + 2³) = a³ - 9a - a³ - 8 = -9a - 8
4/ (a² - 1)(a² + 1)(a⁴⁸ + 1)(a¹² + 1)(a²⁴ + 1)(a⁴ - a² + 1)(a⁴ + a² + 1) = a⁹⁶ - 1
по частям 1. первые 2 скобки 2. 3-4-5 скобки 3. 6 и 7 скобки
(a² - 1)(a² + 1) = a⁴ - 1
(a⁴ - a² + 1)(a⁴ + a² + 1) = (a⁴ + 1 - a² )(a⁴ + 1 + a²) = (a⁴ + 1)² - (a² )² = a⁸ + 2a⁴ + 1 - a⁴ = a⁸ + a⁴ + 1
(a⁴ - 1)(a⁸ + a⁴ + 1) = a¹² - 1
(a¹² - 1)(a⁴⁸ + 1)(a¹² + 1)(a²⁴ + 1) = (a¹² - 1)(a¹² + 1)(a²⁴ + 1)(a⁴⁸ + 1) = (a²⁴ - 1)(a²⁴ + 1)(a⁴⁸ + 1) = (a⁴⁸ - 1)(a⁴⁸ + 1) = a⁹⁶ - 1
Ответ: a⁴⁸ - 1.
Объяснение: