Предмет: Геометрия,
автор: Mari171
С решением, пожалуйста)
Приложения:
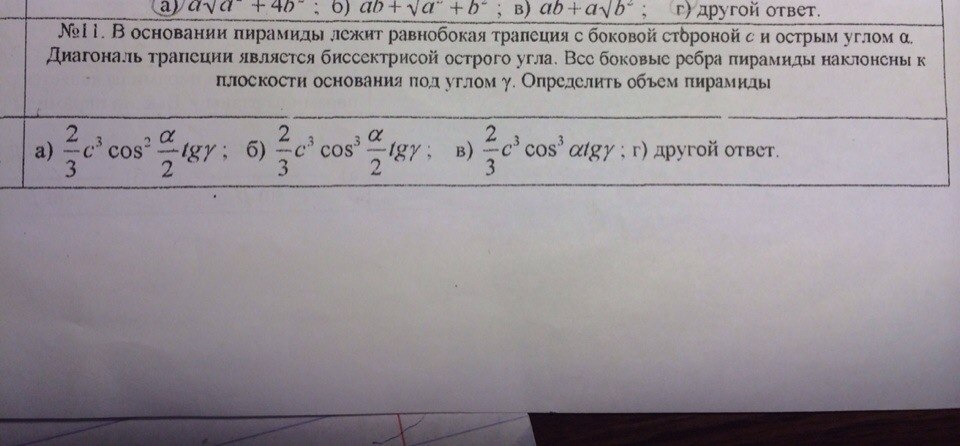
Ответы
Автор ответа:
0
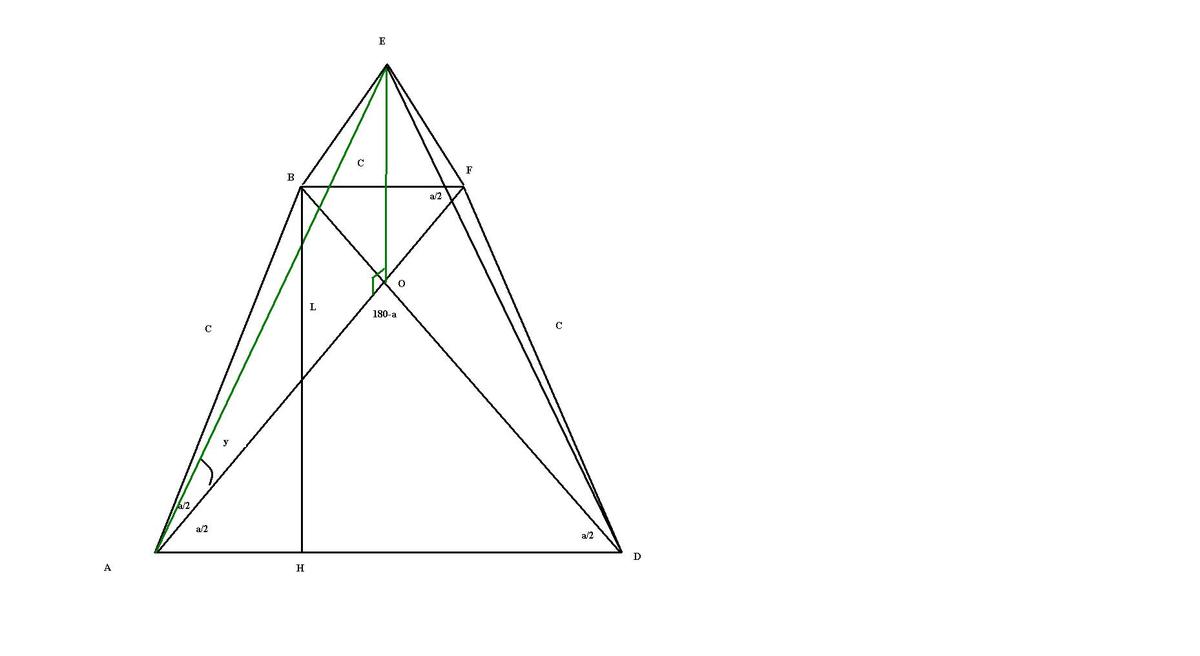
выходит что угол
Так как
Пусть
Приложения:
Похожие вопросы
Предмет: Психология,
автор: Xyixuixyi
Предмет: Математика,
автор: avvaava91
Предмет: История,
автор: elezavetaparfe74
Предмет: Химия,
автор: nikifirova98