Предмет: Геометрия,
автор: fffuucckkk
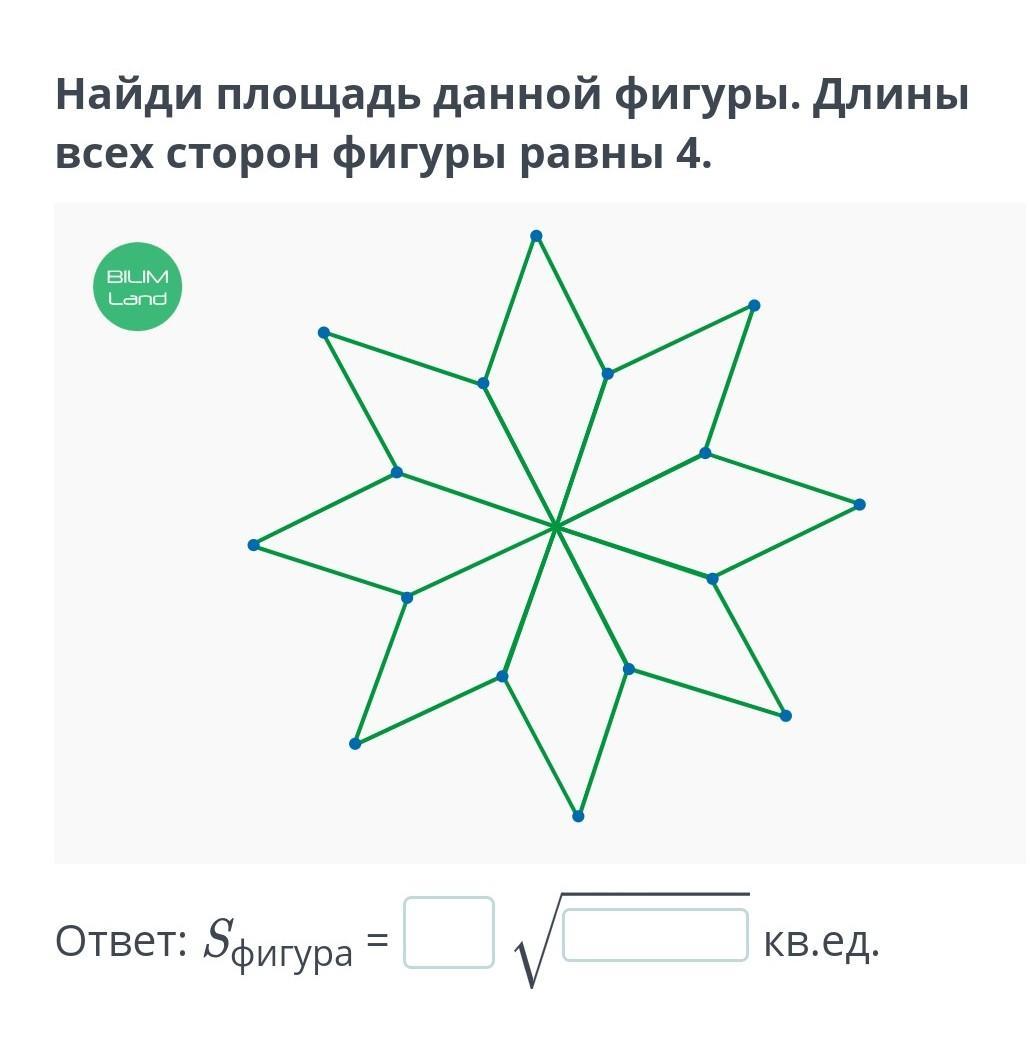
Найди площадь данной фигуры. Длины всех сторон фигуры равны 4.
Приложения:
Ответы
Автор ответа:
1
Ответ:
Sфиг = кв. ед.
Объяснение:
Требуется найти площадь фигуры по представленному рисунку.
1) Фигура состоит из 8 равных ромбов, последовательно соединенных своими острыми углами.
Ромб - это параллелограмм, у которого все стороны равны.
По условию сторона ромба равна 4.
2) Найдем острый угол ромба.
Полный круг составляет 360°. Сторонами ромба он разделен на 8 частей.
Тогда острый угол ромба равен: 360° : 8 = 45°.
3) Найдем площадь одного ромба.
Площадь ромба равна произведению квадрата его стороны на синус острого угла.
Площадь одного ромба равна кв. единиц.
4) А площадь всей фигуры равна площади восьми таких ромбов.
Площадь фигуры равна кв. единиц.
Похожие вопросы
Предмет: Математика,
автор: сонечка02
Предмет: Обществознание,
автор: uzmakka
Предмет: География,
автор: Heeeeyyyy
Предмет: Математика,
автор: Студент000
Предмет: Русский язык,
автор: Знайка2021