Предмет: Алгебра,
автор: meybril
Помогите с примером. Вычислить предел.
Приложения:
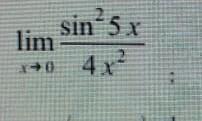
Ответы
Автор ответа:
1
проверим предел при х=0
тогда применим Первое правило Лопиталя
и еще раз правило Лопиталя
Похожие вопросы
Предмет: Алгебра,
автор: theisrussia
Предмет: Математика,
автор: ДумчЕлена
Предмет: Математика,
автор: elenaguk1980
Предмет: Геометрия,
автор: ник2701
Предмет: Химия,
автор: ViproS1