Предмет: Алгебра,
автор: kovalskaya0820
Помогите с примером. Вычислить предел.
Приложения:
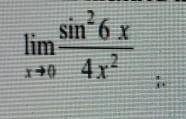
NNNLLL54:
=36/4=9
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
проверим предел при х=0
применим правило Лопиталя (дважды)
Похожие вопросы
Предмет: Математика,
автор: AliceFoxesAd
Предмет: Математика,
автор: korotkevich1981
Предмет: Математика,
автор: nyashik8
Предмет: Литература,
автор: smirnovann
Предмет: Математика,
автор: Ballasniger