Question

Решите систему уравнений СРОЧНО!!!!!
y=4-x
x^2+y^2=10
Определите пересекает ли прямая y=4-x окружность x^2+y^2=10
Если да, то выясните, сколько точек пересечения

Answer 1

Ответ:

Объяснение:

Y=4-x

X²+y²=10

мы находим точки пересечения прямой и окружности, сопоставляя эти уравнения друг с другом

(4-x)²=10-x²

16-8x+x²=10-x²

2x²-8x+6=0  // : 2

X²-4x+3=0

Δ=16-12=4    ;  √Δ=2

X1=(4-2)/2=2/2=1

X2=(4+2)/2=6/2=3

Подставляем полученный x в уравнение y = 4-x, чтобы получить y

Y1=4-1=3

Y2=4-3=1

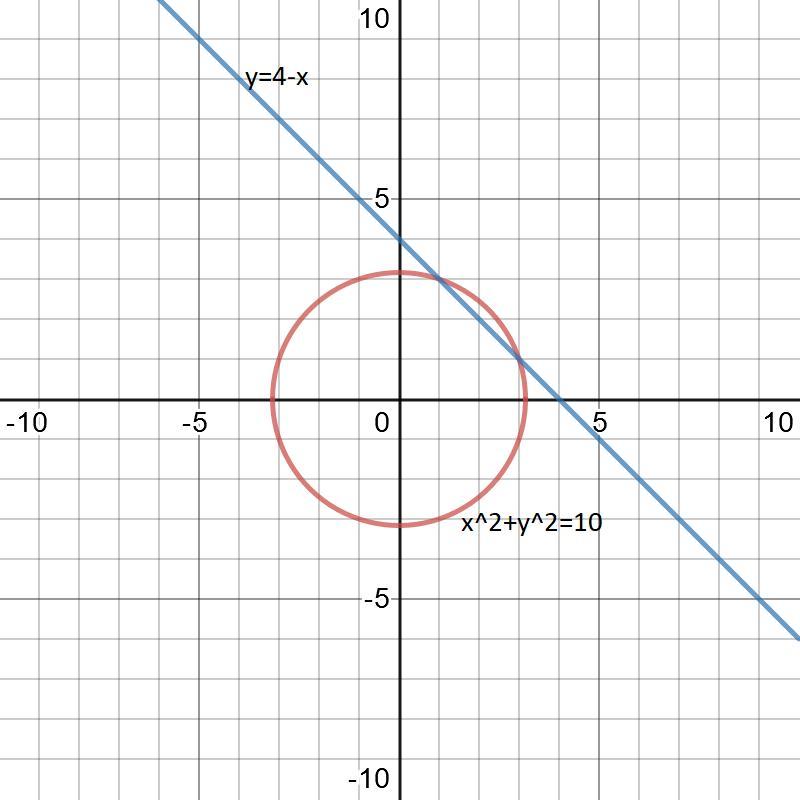
точками пересечения прямой окружности являются (1;3)  i  (3;1), что показано на прилагаемой диаграмме

(Десмос использовался для построения графика)