Question

Сторона квадрата является гипотенузой прямоугольного треугольника, расположенного вне квадрата. Докажите, что биссектриса прямого угла этого треугольника проходит через центр квадрата
срочно, умоляю!.

Answer 1

Здесь нужно использовать свойство биссектрисы как геометрического места точек, равноудаленных от сторон угла. 
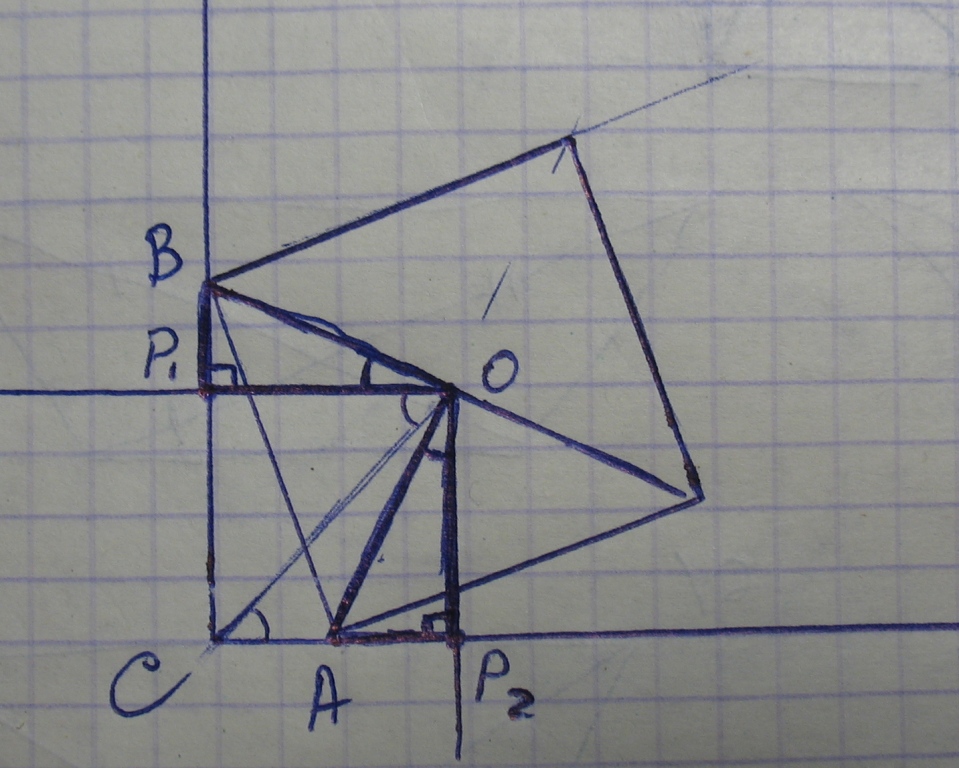
Опустим из центра квадрата перпендикуляры на продолжение катетов прямоугольного треугольника.
Рисунок во вложении.
Рассмотрим треугольники ОВР1 и ОАР2. Они будут равны как прямоугольные треугольники, у которых равны гипотенузы и острый угол: ОА=ОВ (как половины диагонали квадрата) и угол ВОР1= углу АОР2 (так как угол ВОА=90 как угол между диагоналями квадрата, угол Р1ОР2=90 по построению).
Так как треуг. ОВР1 и ОАР2 равны, то имеем равенство сторон Р1О=Р2О.
Значит Р1О и Р2О расстояния от точки О до сторон угла С и они равны между собой, а следовательно точка О является точкой биссектрисы угла С.

Спасибо за интересную задачу :)