Предмет: Математика,
автор: Gsnbdhehs
Найти производные:(см.фото)
Приложения:
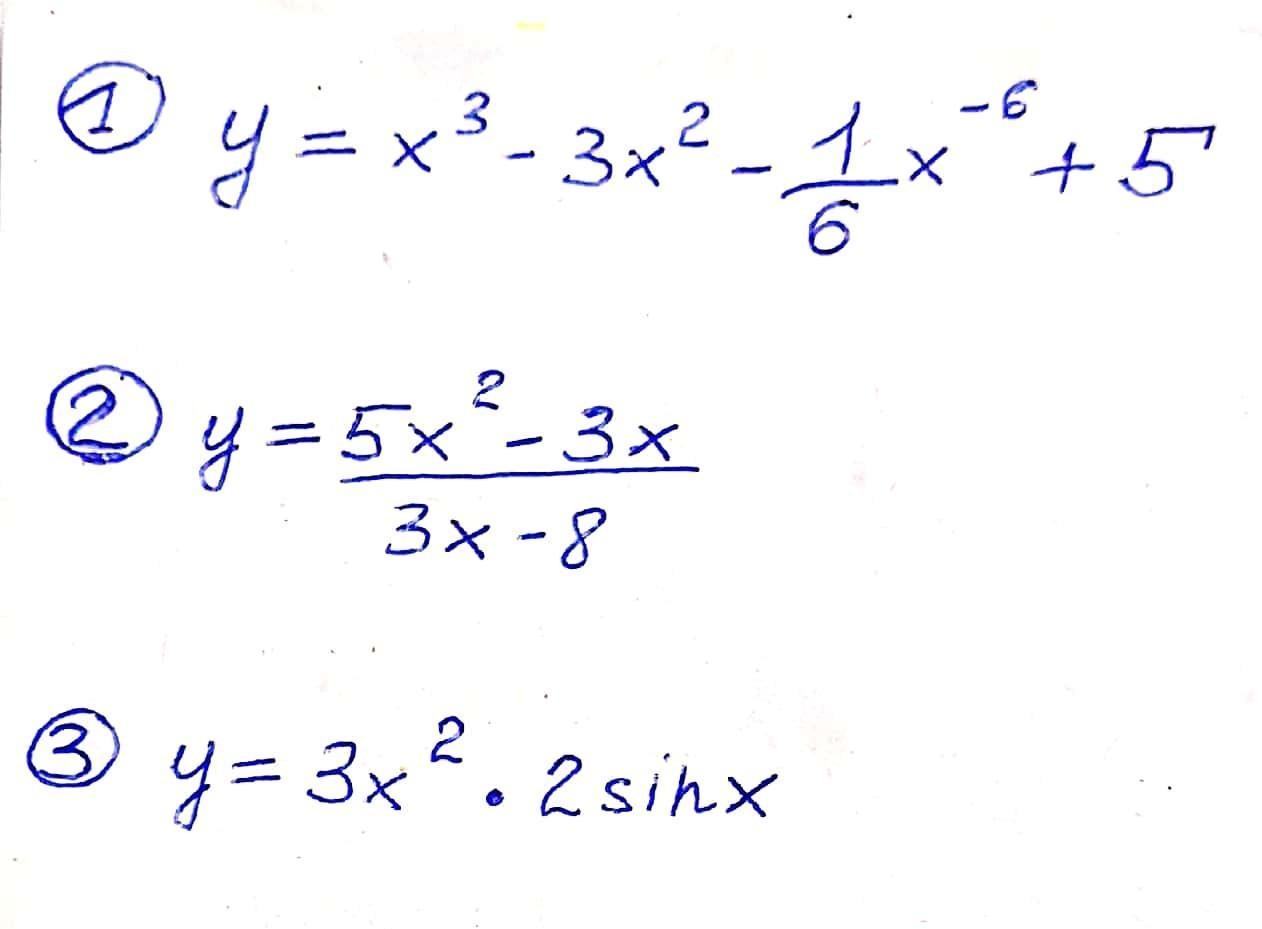
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
1.
2
3
Похожие вопросы
Предмет: Биология,
автор: сепаратисты
Предмет: География,
автор: AlexandraMironova
Предмет: Математика,
автор: lpozdeeva
Предмет: Математика,
автор: daniilstikans