Предмет: Геометрия,
автор: Andreytsy07
ДАЮ 20 БАЛЛОВ! Площади параллелограмма, ромба, квадрата и прямоугольника.
ABCD – параллелограмм. BD – высота, cosA = 3/5
Площадь параллелограмма S = 432 см2.
Найди длины отрезков AD, AB, BD.
Ответ: AD =
см, AB =
см, BD =
см.
Приложения:
Ответы
Автор ответа:
2
Ответ:
AD= 30см, АВ=18см, BD=24см
Объяснение:
BD⟂AB. => треугольник АВD - прямоугольный.
Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе.
AB=3x, AD=5x.
По теореме Пифагора найдём катет BD прямоугольного треугольника АВD:
BD=4x
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
S=AB×BD=432
3x × 4x=432
12x²=432
x²=36
x=6
AB=3x=3×6=18см,
AD=5x=5×6=30см,
BD=4x=4×6=24см.
Приложения:
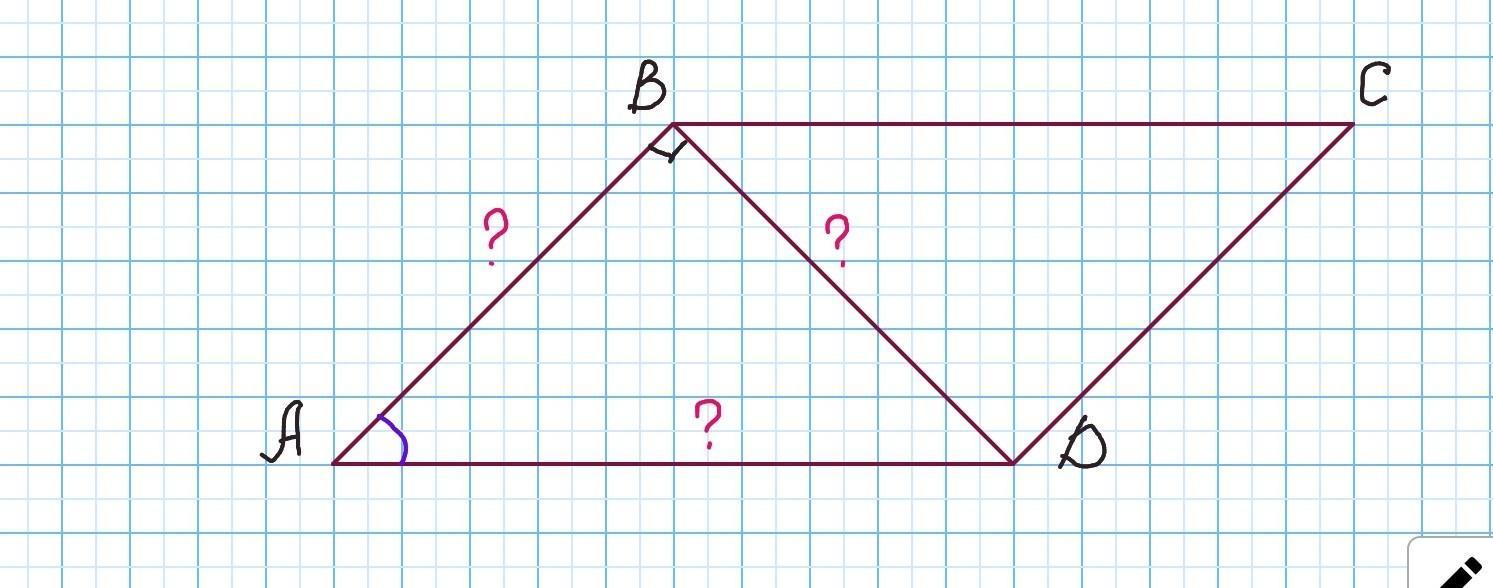
Похожие вопросы
Предмет: Математика,
автор: Боженка10
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: ЛоЛиПА
Предмет: Математика,
автор: Полинаноябрь
Предмет: География,
автор: Элbзабет