Предмет: Алгебра,
автор: fvbjhfvbnhgch
ЗНАТОКИ ПОМОЩЬ НУЖНА.
Найдите наибольшее и наименьшее значения функции третьей степени y=f(x)=ax^3+bx^2+cx+d в указанном интервале.
Приложения:
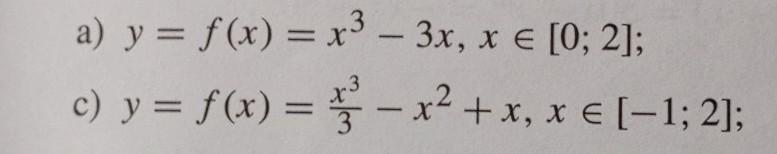
Ответы
Автор ответа:
1
a)
найдем производную
Определим знаки производной
тогда х= -1 точка мах; х=1 точка мин.
На интервале [0;2]
наименьшее значение функции в точке минимума х=1
наибольшее значение либо в точке х=0 или в точке х=2
проверим
тогда максимальное значение равно 2 в точке х=2
с)
найдем производную
Определим знаки производной
значит функция f(x) возрастающая
тогда минимальной значение будет в точке х= -1
тогда максимальное значение будет в точке х=2
Похожие вопросы
Предмет: Химия,
автор: Paul0n
Предмет: Русский язык,
автор: likeman
Предмет: География,
автор: neverovamariya
Предмет: Математика,
автор: den3121516
Предмет: Литература,
автор: irinochka2018