Question

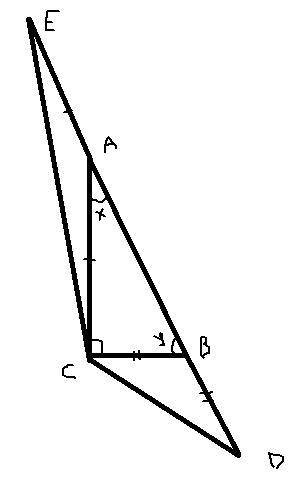
гіпотенузу AB прямокутного трикутника ABC продовжено в обидва боки так, що AE=AC, BD=BC. Точки D і E сполучені з вершиною C. Доведіть, що кут CED+ кут CDE=45

Answer 1

Ответ:

Объяснение:

Пусть <BAC=x, <ABC=y.

AE=AC => △EAC - равнобедренный. => <CEA=<ACE. По свойству внешнего угла <BAC=2*<CEA=x, <CEA=x/2

BD=BC => △СBD - равнобедренный. => <BCD=<BDC. По свойству внешнего угла <ABC=2*<BDC=y, <BDC=y/2.

В прямоугольном △ABC, x+y=90.

Искомая сумма <CED(<CEA)+<CDE(<BDC)=x/2+y/2=1/2*(x+y), а (х+у)=90, значит <CED+<CDE=90/2=45.