Предмет: Алгебра,
автор: ldhrkrd07890
Срочноооооооооо помогитеее мне пж!!!!
Приложения:
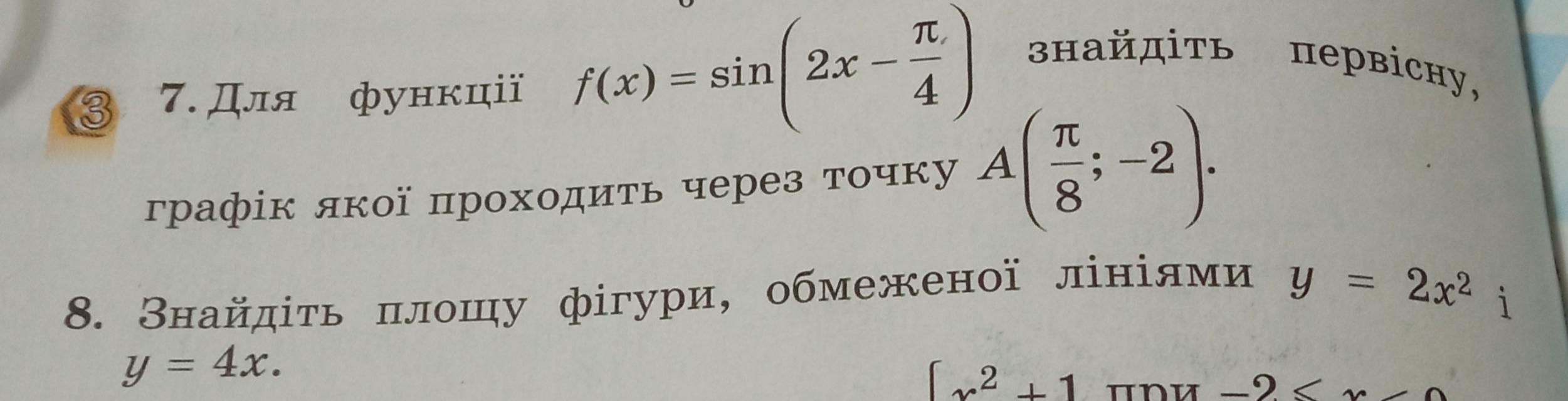
Ответы
Автор ответа:
1
Ответ:
7.
общий вид
в точке А:
8.
Находим площадь, что указана на картинке зеленым цветом.
Для этого найдем разность красной и синей площадей:
S = S1 - S2
Сначала найдем пределы.
Для этого приравняем функции и найдем нули
Ответ: 8/3
Приложения:

Похожие вопросы
Предмет: Математика,
автор: halimahamidova
Предмет: Литература,
автор: 20942094
Предмет: Қазақ тiлi,
автор: EnglandBlackBird
Предмет: История,
автор: азерин1
Предмет: Информатика,
автор: Sabzina505