помогите алгебра срочно прошу
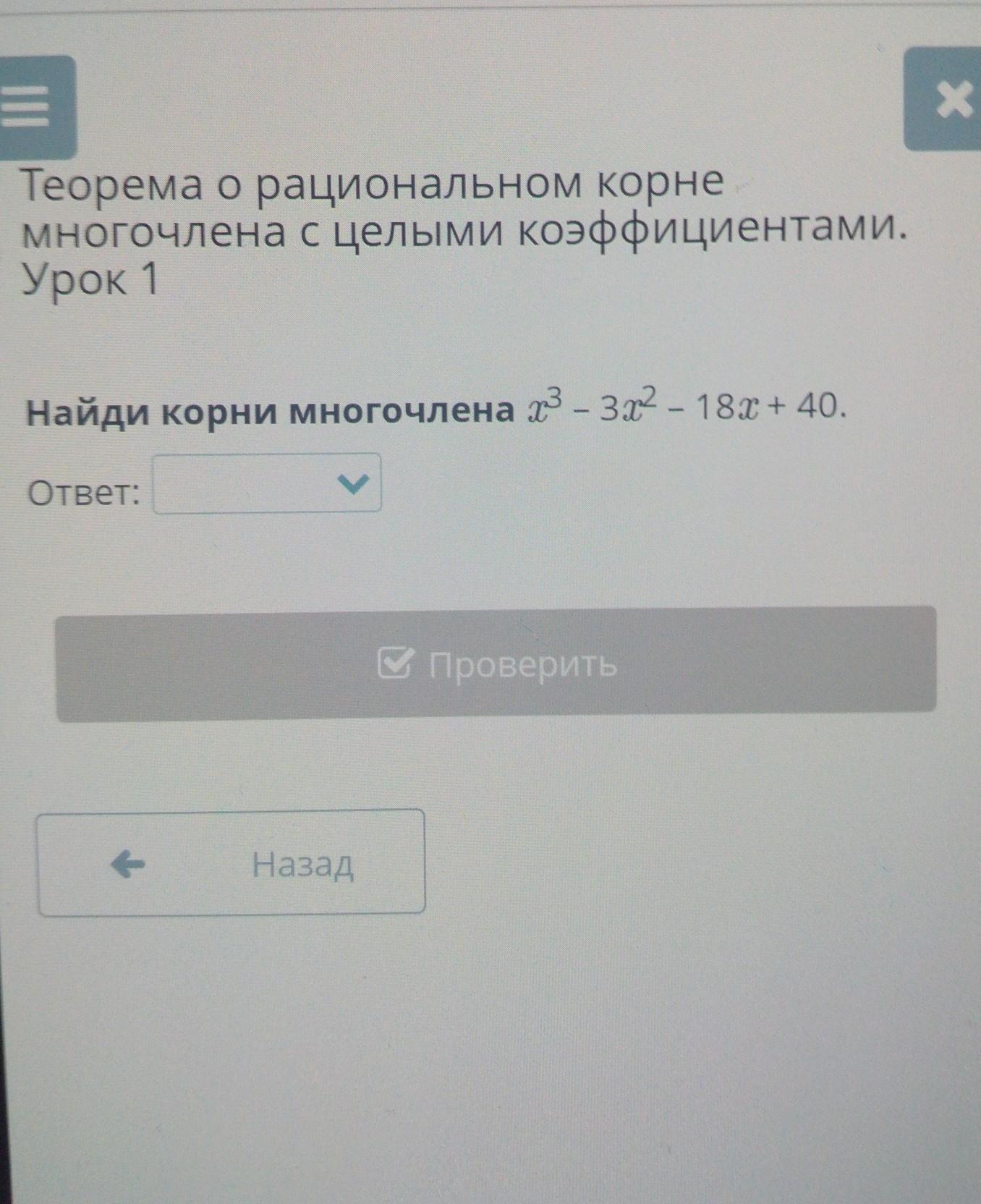
Ответы
Ответ:
x ∈ {-4; 2; 5}
Объяснение:
1. Выбираем один из корней многочлена, как один из целых множителей свободного члена. Вобщем, множителей у числа 40 много, но подстановкой определяем, что подходит число 2:
x³-3x²-18x+40=0 при х=2: 2³-3*2²-18*2+40=0
Итак, один из корней х₁=2. Следовательно наш многочлен можно разложить на множиели следующим образом:
(x-2)(ax²+bx+c)=0;
2. Для определения коэффициентов квадратного трехчлена разделим исходный могочлен 3-й степени на первый множитель (x-2) (в столбик, как обычные числа):
x³-3x²-18x+40 l x-2
x³-2x² l x²-x-20
-x²-18x
-x²+2x
-20x+40
-20x+40
0
(x-2)(x²-x-20)=0;
x²-x-20=0; √D=√(1+80)=9;
x₂₃=0,5(1±9);
x₂=5; x₃=-4; x²-x-20=(x-5)(x+4);
x³-3x²-18x+40=(x-2)(x-5)(x+4);
x∈{-4; 2; 5}.