Question

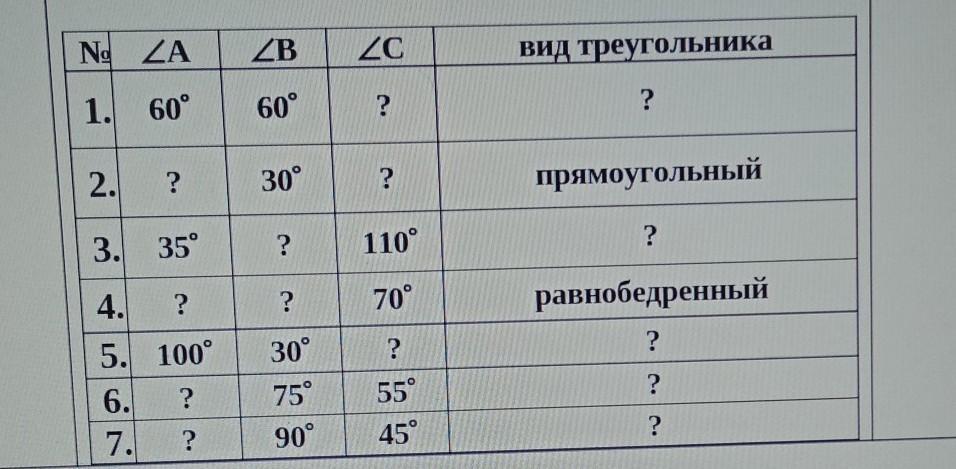
N. ZA
ZB
ZC
вид треугольника
1. 60°
60°
?
?
?
30°
?
прямоугольный
сус
3. 35°
?
110°
?
4.
?
?
70°
равнобедренный
5. 100°
30°
?
?
?
75°
?
6.
7.
55°
45°
?
90°
? даю 70баллов мне надо сегодня сдать прошу помогите пожалуйста!!!!!!!!!!!​

Answer 1

Ответ:

на рисунке

Объяснение:

Сумма углов треугольника равна 180°.

Углы при основании равнобедренного треугольника равны.

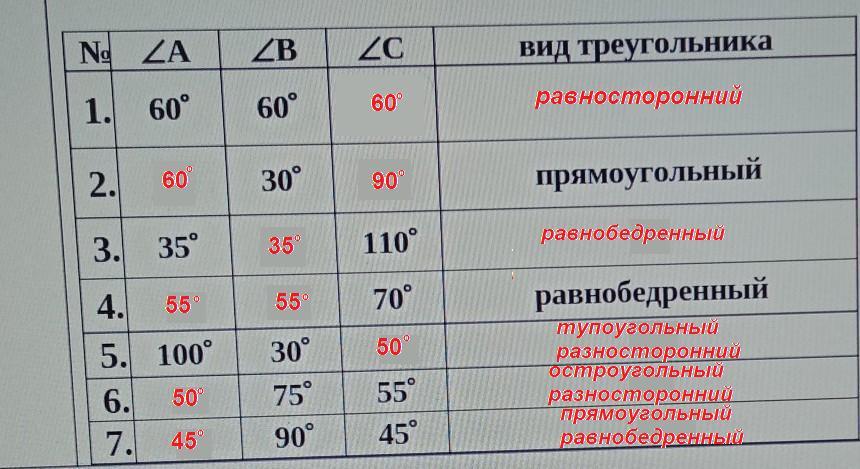
1.

∠А = 60°, ∠В = 60°

∠С = 180° - (∠А + ∠В) = 180° - (60° + 60°) = 180° - 120° = 60°

Если все углы треугольника равны, то он равносторонний.

2.

ΔАВС - прямоугольный, ∠В = 30°

Один из углов должен быть прямым, пусть это будет угол С:

∠С = 90°

Сумма острых углов прямоугольного треугольника равна 90°. Тогда

∠А = 90° - ∠В = 90° - 30° = 60°

3.

∠А = 35°, ∠С = 110°

∠В = 180° - (∠А + ∠С) = 180° - (35° + 110°) = 180° - 145° = 35°

Если в треугольнике два угла равны, то он равнобедренный.

4.

ΔАВС - равнобедренный, ∠С = 70°

Если ∠С - угол при вершине треугольника, то

∠А = ∠В = (180° - ∠С) : 2 = (180° - 70°) : 2 = 110° : 2 = 55°

*Но, если ∠С - угол при основании, то возможны и другие варианты:

• основание АС,

       ∠А = ∠С = 70°,

       ∠В = 180° - (2 · 70°) = 180° - 140° = 40°

• основание ВС:

        ∠В = ∠С = 70°

        ∠А = 180° - (2 · 70°) = 180° - 140° = 40°

5.

∠А = 100°, ∠В = 30°

∠С =  180° - (∠А + ∠В) = 180° - (100° + 30°) = 180° - 150° = 50°

ΔАВС - тупоугольный, разносторонний.

6.

∠В = 75°, ∠С = 55°

∠А =  180° - (∠В + ∠С) = 180° - (75° + 55°) = 180° - 130° = 50°

ΔАВС - остроугольный, разносторонний.

7.

∠В = 90°, ∠С = 45°

Сумма острых углов прямоугольного треугольника равна 90°. Тогда

∠А = 90° - ∠С = 90° - 45° = 45°

ΔАВС - прямоугольный, равнобедренный.