Question

Сумма углов треугольника. Внешний угол треугольника. Урок 2

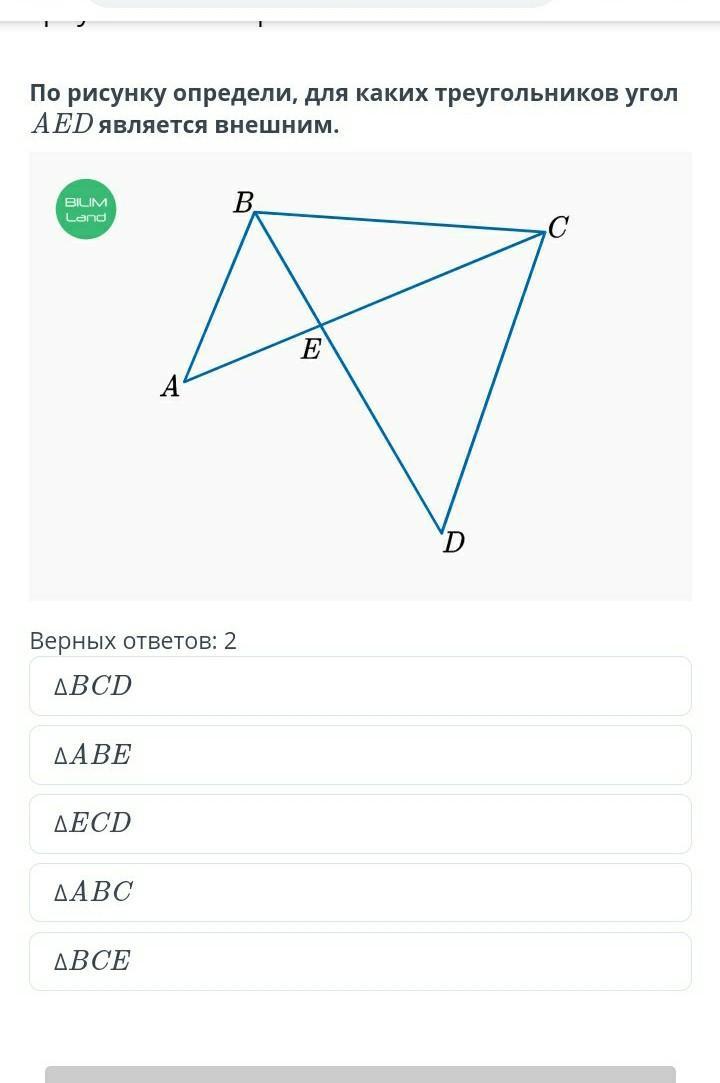
По рисунку определи, для каких треугольников угол AED является внешним.


Верных ответов: 2

∆BCD

∆ABE

∆ECD

∆ABC

∆BCE



​

Answer 1

Ответ:

ΔABE, ∆ECD

Объяснение:

По определению внешний угол треугольника это угол, смежный с любым из внутренних углов треугольника.

1) ΔABE

Так как угол ∠BEA смежный с углом ∠AED, то по определению внешнего угла, угол ∠AED является внешним для треугольника ΔABE.

2) ∆ECD

Так как угол ∠CED смежный с углом ∠AED, то по определению внешнего угла, угол ∠AED является внешним для треугольника ΔECD.

Answer 2

Ответ:

△АВЕ

△ЕСD

Объяснение:

• Внешний угол треугольника – это угол, смежный с любым из внутренних углов треугольника. 
• Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют в сумме 180°.

∠AED и ∠АЕВ - смежные углы, т.к. АЕ-общая, ВЕ и ED - лежат на одной прямой.

∠АЕВ - внутренний угол △АВЕ.

Следовательно ∠AED внешний угол для △АВЕ.

∠AED и ∠CED - смежные углы, т.к. ЕD-общая, AЕ и EC - лежат на одной прямой.

∠CЕD - внутренний угол △ЕCD.

Следовательно ∠AED внешний угол для △ECD.