Предмет: Геометрия,
автор: Аноним
помогите пожалуйста.
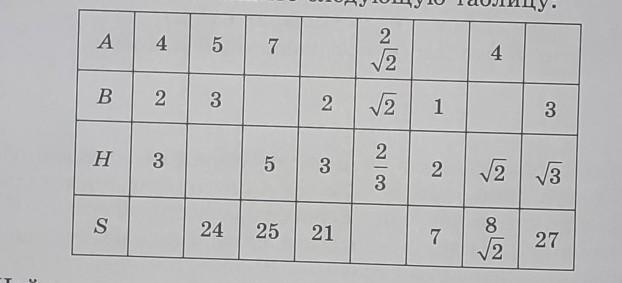
пусть S - площадь трапеции, а и b - основания, h - высота, проведённая к основанию. заполните следующую таблицу.
Приложения:
Ответы
Автор ответа:
42
Ответ:
на рисунке
Объяснение:
Формула площади трапеции с основаниями а и b и высотой h:
(1)
Выразим высоту:
(2)
Из формулы площади выразим основание:
или
(3)
1) a = 4, b = 2, h = 3
Применим формулу (1):
2) a = 5, b = 3, S = 24
Применим формулу (2):
3) a = 7, h = 5, S = 25
Применим формулу (3):
4) b = 2, h = 3, S = 21
Применим формулу (3):
5)
Применим формулу (1):
6) b = 1, h = 2, S = 7
Применим формулу (3):
7) a = 4, h = √2, S = 8√2
Применим формулу (3):
8) b = 3, h = √3, S = 27
Применим формулу (3):
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Rocky8
Предмет: Математика,
автор: silaevaira78
Предмет: Математика,
автор: valef2012
Предмет: Математика,
автор: VAIERKA