Question

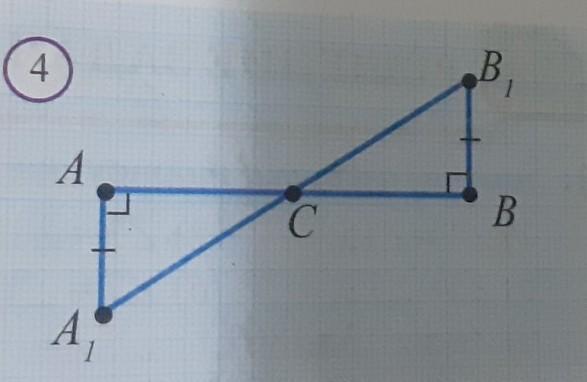
Покажите, что АС=СВ на рисунке 4.​

Answer 1

Ответ:

AA$_{1}$ || BB$_{1}$, т.к. они оба пересекают отрезок AB под прямым углом.

Значит внутренние накрест лежащие углы AA$_{1}$C и BB$_{1}$C равны.

Т.к. катеты AA$_{1}$ = BB$_{1}$ и углы AA$_{1}$C=BB$_{1}$C, то по второму признаку равенства прямоугольных треугольников: если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны. Значит и вторые катеты у этих треугольников тоже равны между собой: AC=CB.