Предмет: Математика,
автор: erkinzhoro
Найти производную dx dy от функции, заданной параметрически.
Приложения:
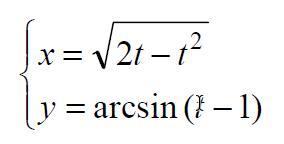
Ответы
Автор ответа:
3
Ответ:
Похожие вопросы
Предмет: Математика,
автор: katyahamster
Предмет: Литература,
автор: markelovayulya
Предмет: Математика,
автор: varvarkir
Предмет: Литература,
автор: kekoiuy