Предмет: Геометрия,
автор: aronova121219
26 баллов!!!
Точка S равноудалена от сторон трапеции АВCD (ВС || AD) и находится на расстоянии Корень из 7 см от её пло- скости. Найдите расстояние от точки S до сторон трапеции, если CD=12 см, А угол ADC=45°
Ответы
Автор ответа:
6
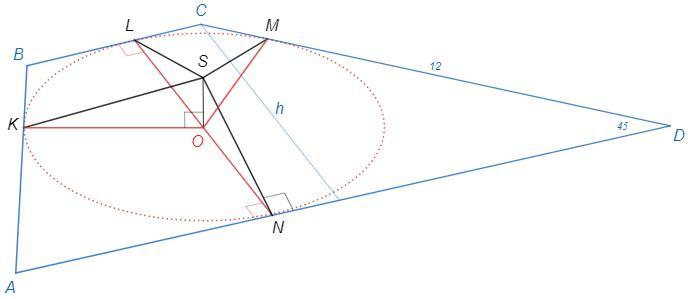
Опустим перпендикуляр SO на плоскость трапеции, SO=√7
Пусть SN - расстояние до стороны AD, SN⊥AD
Тогда по теореме о трех перпендикулярах ON⊥AD
Аналогично OK, OL, OM - расстояния от O до сторон трапеции.
Наклонные из точки S равны, следовательно равны их проекции.
Точка O равноудалена от сторон трапеции и является центром вписанной окружности.
Диаметр вписанной окружности трапеции равен высоте.
LN =h =CD sin45 =12 √2/2 =6√2
ON =LN/2 =3√2
△SON, т Пифагора
SN =√(SO^2 +ON^2) =√(7+18) =5 (см)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: tatiananet85
Предмет: Математика,
автор: 11199
Предмет: Русский язык,
автор: samorodnyayasvetlana
Предмет: Химия,
автор: leravolk399