Предмет: Математика,
автор: nikitina2016153
вычислите пределы под а)б)в)г)
Приложения:
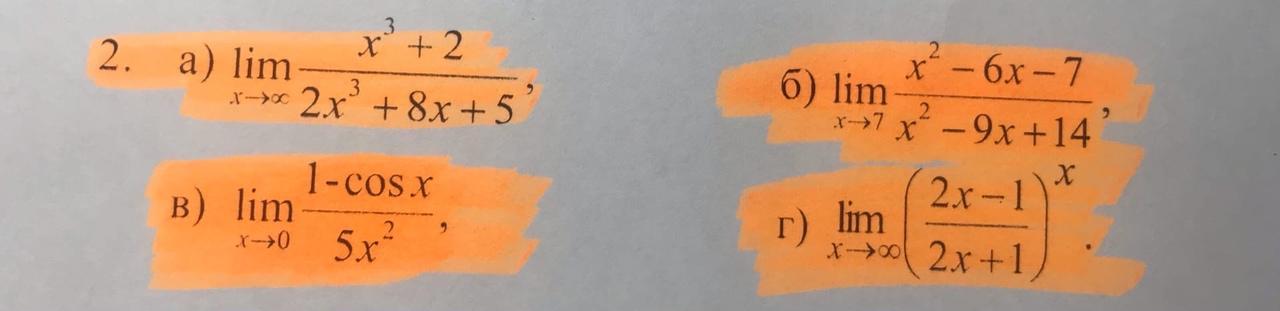
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
а)
б)
так как числитель и знаменатель обращаются в нуль при x=7, то 7 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x - 7) .
x² -6x -7 = (x-7)(x+1)
x² - 9x +14 = (x-7)(x-2)
и тогда получим
в)
1-cos = 2sin²(x/2)
следствию свойства первого замечательного предела
sinx ≈ x, тогда 2sin²(x/2) ≈x²/2
и вот что получилось
г)
здесь применим свойство второго замечательного предела
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Вероника376
Предмет: Другие предметы,
автор: магдафон
Предмет: География,
автор: angelinagrigor1
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: Ratatuile