Предмет: Геометрия,
автор: Sverhchelovechek
ДАЮ 100 БАЛЛОВ
У правильному тетраедрі ABCD CM=MB ( M∈CB ) . Знайдіть кут між прямими AM і BD.
Ответы
Автор ответа:
4
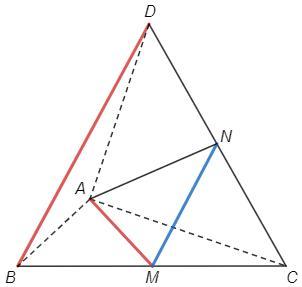
В правильном тетраэдре ABCD точка M - середина BС. Найдите угол между прямыми AM и BD.
Прямая BD пересекает плоскость (ABC) в точке, не лежащей на прямой AM - прямые AM и BD скрещиваются.
Угол между скрещивающимися прямыми - угол между параллельными им пересекающимися прямыми.
Проведем MN||BD
∠AMN - искомый угол.
Правильный тетраэдр, все грани - правильные треугольники.
Пусть все ребра равны а
N - середина CD (т Фалеса)
MN=a/2 (средняя линия)
AM=AN =a√3/2 (медианы в равностороннем треугольнике)
△MAN - равнобедренный
cos(AMN) =MN/2AM =2a/4a√3 =√3/6
∠AMN =arccos(√3/6)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Малая33
Предмет: Литература,
автор: khristina2
Предмет: Русский язык,
автор: anyuta08102004
Предмет: Математика,
автор: алларазмяу
Предмет: География,
автор: vladkakornulyk